%%{init: {'flowchart': {'curve': 'stepAfter'}}}%%
graph LR
classDef hidden fill:none,stroke:none,width:0px,height:0px
A1(随机事件和概率)
M1[ ]:::hidden
A1 --- M1
M1 --> B1(基本概念)
M1 --> B2(事件的关系与运算)
M1 --> B3(古典概型与几何概型)
M1 --> B4(概率的定义与性质)
M1 --> B5(条件概率)
M1 --> B6(事件独立性)
M1 --> B7(全概率公式与贝叶斯公式)
M1_2[ ]:::hidden
B1 --- M1_2
M1_2 --> C1_1(随机试验)
M1_2 --> C1_2("样本点、样本空间")
M1_2 --> C1_4(随机事件)
M1_2 --> C1_7(事件发生)
M1_3[ ]:::hidden
C1_4 --- M1_3
M1_3 --> C1_3(基本事件)
M1_3 --> C1_5(不可能事件)
M1_3 --> C1_6(必然事件)
M2_2[ ]:::hidden
B2 --- M2_2
M2_2 --> C2_1("包含、相等、和差、互斥、对立")
M2_2 --> C2_2("交换律、结合律、分配律、对偶律")
M4_2[ ]:::hidden
B4 --- M4_2
M4_2 --> C4_1("统计定义、公理化定义")
M4_2 --> C4_2("非负性、规范性、有限可加性")
M4_2 --> C4_3("加法公式、减法公式")
B5 --> C5_1(乘法公式)
M6_2[ ]:::hidden
B6 --- M6_2
M6_2 --> C6_1(两个事件)
M6_2 --> C6_2(多个事件)
M7_2[ ]:::hidden
B7 --- M7_2
M7_2 --> C7_1(完备事件组)
M7_2 --> C7_2(抽签原理)
我整理了物理光学的 PDF 版复习资料(包含薄膜干涉、偏振、衍射、双缝干涉),欢迎点击下方链接下载:
概率论期末备考
以下内容均来自 【【Kira老师】《概率论与数理统计》大学生零基础精讲课25h(已完结)| 26考研基础阶段适用】 我只会列出我觉得重要的点,应付期末考试是足够的
第一章-随机事件和概率
1-1. 随机事件与样本空间
内容比较简单,略过
1-2. 随机事件与样本空间
选择题考了要能知道是在说什么事件并且要知道公式
差事件: \(A - B = A\overline{B}\) 表示A发生B不发生
互斥事件也就是互不相容事件
互逆事件也就是对立事件
交换律: \(A \cup B = B \cup A\),\(A \cap B = B \cap A\)
结合律: \(A \cup (B \cup C) = (A \cup B) \cup C\),\(A \cap (B \cap C) = (A \cap B) \cap C\)
分配律: \(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\),\(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\)
例题:设 \(A,B\) 是两个随机事件,则 \((A \cup B)(\overline{A} \cup \overline{B}) =\) 点击查看答案\(A \overline{B} + \overline{A} B\) 点击跳转到视频讲解链接
- 对偶律(德摩根律): \(\overline{A \cup B} = \overline{A} \cap \overline{B}\), \(\overline{A \cap B} = \overline{A} \cup \overline{B}\) ,简单来讲就是长横变短横,交和并互化
例题:以 \(A\) 表示事件”甲产品畅销,乙产品滞销”,则其对立事件 \(\overline{A}\) 为 点击查看答案D
| (A)甲产品畅销,乙产品滞销; | (B)甲、乙两种产品均畅销; |
| (C)甲产品滞销; | (D)甲产品滞销或乙产品畅销 |
1-3. 古典概型
古典概型简单来讲就是样本空间中的样本点出现的可能性相同
置球入盒模型,建议看视频讲解,我觉得很重要 点击跳转到视频讲解链接
1-4. 几何概型
几何概型简单来讲就是把古典概型扩展了一下,将等可能事件的概念从有限到无限延伸
例题:若在区间(0,1)内任取两个数,则事件”两数之和小于 \(\frac{6}{5}\)” 发生的概率为 点击查看答案\(\frac{17}{25}\)
1-5. 概率的概念和基本性质
概率论的基本功,要掌握
例题:如果事件 \(A\) 与 \(B\) 同时发生的概率为 \(P(AB) = 0\) ,则 点击查看答案D
|
|
|
|
不要想当然的以为AB是不可能事件,概率为0的事件也会发生,概率为1的事件也有可能不发生,一般来说,概率推事件是不对的
有限可加性:若事件 \(A_1, A_2, \dots, A_n\) 两两互斥,则 \(P\left(\bigcup_{i=1}^{n} A_i\right) = \sum_{i=1}^{n} P(A_i)\)
减法公式:对于任意两个随机事件 \(A\) 和 \(B\) ,有 \(P(A - B) = P(A) - P(AB)\)
加法公式:对于任意两个随机事件 \(A\) 和 \(B\) ,有 \(P(A + B) = P(A) + P(B) - P(AB)\)
例题:试比较 \(P(A), P(AB), P(A+B), P(A) + P(B)\) 的大小 点击查看答案\(P(AB) \le P(A) \le P(A+B) \le P(A) + P(B)\)
例题:\(A\) , \(B\) 是两随机事件,\(P(AB) = P(\overline{A} \ \overline{B}), \quad P(A) = p\),则 \(P(B)\) = 点击查看答案\(1 - p\)
1-6. 条件概率
同样比较基础,也得会
条件概率定义:设 A, B 为两个事件,若 P(B) > 0,称 \(P(A|B) = \frac{P(AB)}{P(B)}\) 为事件 B 发生条件下事件 A 发生的条件概率。
可列可加性:对两两互斥的事件列 \(A_1, A_2, \ldots, A_n, \ldots\), 有 \(P\left(\bigcup_{i=1}^{\infty} A_i \mid B\right) = \sum_{i=1}^{\infty} P(A_i \mid B)\)
加法公式和减法公式和上一节的一样,但是要带上 \(|\) 下面的字母
例题:设 A, B 是两随机事件,\(P(A) = 0.4, P(B) = 0.3, P(A|B) = 0.5\),则 \(P(A \cup B)\) = 点击查看答案\(0.55\)
例题:某人忘记了电话号码的最后一个数字,因此他随意地拨号。
求他不超过三次能打通所需电话的概率 点击查看答案\(\frac{3}{10}\)
若已知最后一个数字是奇数,求他不超过三次能打通所需电话的概率 点击查看答案\(\frac{3}{5}\)
1-7. 事件间的独立性
二级结论比较多
设 A 与 B 是两事件,如果满足等式 \(P(AB) = P(A)P(B)\),称事件 A 与 B 相互独立,简称 A, B 独立。
若事件 A 与事件 B 相互独立,则 \(A\) 与 \(\overline{B}\),\(\overline{A}\) 与 \(B\),\(\overline{A}\) 与 \(\overline{B}\) 亦相互独立。
若不说明 \(0 < P(A) < 1, 0 < P(B) < 1\),则 A 与 B 是否独立和 A 与 B 是否互斥无必然联系。在概率不为 0 或 1 的情况下,独立一定不互斥,互斥一定不独立
例题:设 \(A\) 与 \(B\) 互斥(互不相容),则下列结论中正确的是 点击查看答案D
| A. \(\overline{A}\) 与 \(\overline{B}\) 互斥 | B. \(\overline{A}\) 与 \(\overline{B}\) 相容 |
| C. \(A\) 与 \(B\) 不独立 | D. \(P(A\overline{B}) = P(A)\) |
- 三个事件的独立性:称事件 \(A, B, C\) 两两独立,如果
\[ \begin{cases} P(AB) = P(A)P(B) \\\\ P(BC) = P(B)P(C) \\\\ P(AC) = P(A)P(C) \end{cases} \]
进一步如果满足等式 \(P(ABC) = P(A)P(B)P(C)\),则称事件 \(A, B, C\) 相互独立
注:相互独立的随机事件 \(A_1, A_2, \dots, A_n\) 中,任何一部分事件的和、差、积、逆运算结果,都与另一部分独立。
例如 \(\overline{A \cup B}\) 与 \(C\),\(A - B\) 与 \(C\),\(A\) 与 \(BC\),他们都是相互独立的
1-8. 全概率公式和贝叶斯公式
高中学过,直接看题目
例题:某人到武汉参加会议,他乘火车、轮船、汽车或飞机去的概率分别为0.2,0.1,0.3和0.4。如果他乘火车、轮船、汽车前去,迟到的概率分别为 \(\frac{1}{3}\),\(\frac{1}{12}\),\(\frac{1}{4}\),乘飞机不会迟到。结果他迟到了,求他是乘汽车去的概率。点击查看答案\(\frac{1}{2}\)
例题:将两信息分别为 \(A,B\) 发送出去,接收站收到时,\(A\) 被误收作 \(B\) 的概率为0.04,而 \(B\) 被误收作 \(A\) 的概率为0.07,信息 \(A\) 与信息 \(B\) 传送频繁程度为3:2。若已知接收到的信息是 \(A\),求原发信息也是 \(A\) 的概率。点击查看答案\(\frac{144}{151}\)
第二章-随机变量及其分布
%%{init: {'flowchart': {'curve': 'stepAfter'}}}%%
graph LR
classDef hidden fill:none,stroke:none,width:0px,height:0px
A2(随机变量及其分布)
N1[ ]:::hidden
A2 --- N1
N1 --> D1(随机变量)
N1 --> D2(分布函数)
N1 --> D3(常见离散型随机变量分布)
N1 --> D4(常见连续型随机变量分布)
N1 --> D5("随机变量函数 Y=g(X) 的分布")
N2[ ]:::hidden
D1 --- N2
N2 --> E1_1(离散型)
N2 --> E1_2(连续型)
N2 --> E1_3(非离散非连续型)
E1_1 --> F1_1(分布律)
E1_2 --> F1_2(概率密度)
N3[ ]:::hidden
D2 --- N3
N3 --> E2_1(定义)
N3 --> E2_2(性质)
N4[ ]:::hidden
D3 --- N4
N4 --> E3_1(二项分布)
N4 --> E3_2(0-1分布)
N4 --> E3_3(泊松分布)
N4 --> E3_4(几何分布)
N4 --> E3_5(超几何分布)
E3_3 --> F3_1(泊松定理)
N5[ ]:::hidden
D4 --- N5
N5 --> E4_1(均匀分布)
N5 --> E4_2(指数分布)
N5 --> E4_3(正态分布)
N6[ ]:::hidden
D5 --- N6
N6 --> E5_1(离散型X)
N6 --> E5_2(连续型X)
N7[ ]:::hidden
E5_2 --- N7
N7 --> F5_1(分布函数法)
N7 --> F5_2(公式法)
2-1. 随机变量
内容比较简单,略过
2-2. 分布函数
所有随机变量都有分布函数,连续型随机变量的分布函数是处处连续的,离散型随机变量的分布函数的有跳跃间断点的
分布函数定义:设 \(X\) 是一个随机变量, \(x\) 是任意实数,函数 \[ F(x) = P\{X \le x\}, -\infty < x < +\infty \] 称为 \(X\) 的分布函数. 它表示 \(X\) 的取值落在实数 \(x\) 左侧的概率,所有的随机变量 \(X\) 都有分布函数 \(F(x)\)
\(P\{X \le a\} = F(a)\); \(P\{X < a\} = F(a-0)\);
分布函数 \(F(X)\) 的基本性质:
- 非负性:\(0 \le F(x) \le 1\).
- 单调性:\(F(x)\) 是 \(x\) 的单调不减函数,即对 \(\forall x_1 < x_2\),有 \(F(x_1) \le F(x_2)\).
- 规范性:\(F(-\infty) = \lim_{x \to -\infty} F(x) = 0\), \(F(+\infty) = \lim_{x \to +\infty} F(x) = 1\).
- 右连续性:\(F(x_0) = F(x_0 + 0)\).
2-3. 离散型随机变量
离散型随机变量就不讲了,比较简单,要记住的是:只有离散型才有分布律,有分布律的一定是离散型
2-4. 二项分布 \(X \sim B(n, p)\)
高中学过,这里简单回顾一下
定义:随机变量 \(X\) 表示 \(n\) 重伯努利试验中事件 \(A\) 发生的次数。记每次试验中事件 \(A\) 发生的概率为 \(p\),则 \(X\) 的分布律为
\[ P\{X = k\} = C_n^k p^k (1-p)^{n-k}, (k = 0, 1, ..., n) \]
其中 \(0<p<1\),则称 \(X\) 服从参数为 \(n, p\) 的二项分布,记为 \(X \sim B(n, p)\)
2-5. \(0-1\) 分布、几何分布 \(X \sim Ge(p)\)
0-1分布就是随机变量X只能取0,1的特殊二项分布 几何分布就是前面几次试验都失败,最后一次成功的二项分布
几何分布公式: \[ P\{X = k\} = (1-p)^{k-1}p, (k = 1, 2, ...) \]
其中 \(0<p<1\),则称 \(X\) 服从几何分布,记作 \(X \sim Ge(p)\)
2-6. 泊松分布 \(X \sim P(\lambda)\)
这个考点题目一般会很直白的说出来X服从泊松分布
泊松分布 \(P(\lambda)\):设随机变量 \(X\) 所有可能取的值为 \(0, 1, 2, ...\),其分布律为
\[ P\{X = k\} = \frac{\lambda^k e^{-\lambda}}{k!}, (k = 0, 1, 2, ...) \]
当二项分布中 \(n\) 很大 \(p\) 很小时,二项分布可以近似成泊松分布,此时 \(\lambda = np\),注意,要题目说了才能这样近似
2-7. 超几何分布 \(X \sim H(n, M, N)\)
高中学过,简单回顾下
超几何分布的分布律: \[ P\{X = k\} = \frac{C_M^k C_{N-M}^{n-k}}{C_N^n}, k = max\{0, n - N + M\}, ..., min\{n, M\} \]
2-8. 连续型随机变量
只有连续型随机变量才有概率密度 \(f(x)\) ,有概率密度 \(f(x)\) 的一定是连续型随机变量
\(F(x) = \int_{-\infty}^{x} f(t) dt\),其中 \(f(x)\) 不一定要连续,可积就行了,但 \(F(X)\) 必须要处处连续
\(P\{X = a\} = 0,P\{a < X \le b\} = P\{a \le X < b\} = P\{a \le X \le b\} = P\{a < X < b\}\).连续型随机变量不用在意等号
概率密度 \(f(x)\) 的性质:
- 非负性:\(f(x) \ge 0\).
- 规范性:\(\int_{-\infty}^{+\infty} f(x) dx = 1\).
- 对于任意实数 \(a, b\), \(a \le b\),有 \(P\{a < X \le b\} = F(b) - F(a) = \int_{a}^{b} f(x) dx\).
- 若 \(f(x)\) 在点 \(x\) 连续,则有 \(F'(x) = f(x)\).
2-9. 均匀分布 \(X \sim U(a,b)\)
均匀分布的概率密度:\(f(x) = \begin{cases} \frac{1}{b-a}, & a < x < b, \\\\ 0, & 其他, \end{cases}\)
均匀分布的分布函数:\(F(x) = \begin{cases} 0, & x < a, \\\\ \frac{x-a}{b-a}, & a \le x < b, \\\\ 1, & x \ge b. \end{cases}\)
计算技巧:
假设 \(X \sim U(-1, 2)\) , 求 \(P\{X \ge 0\}\)
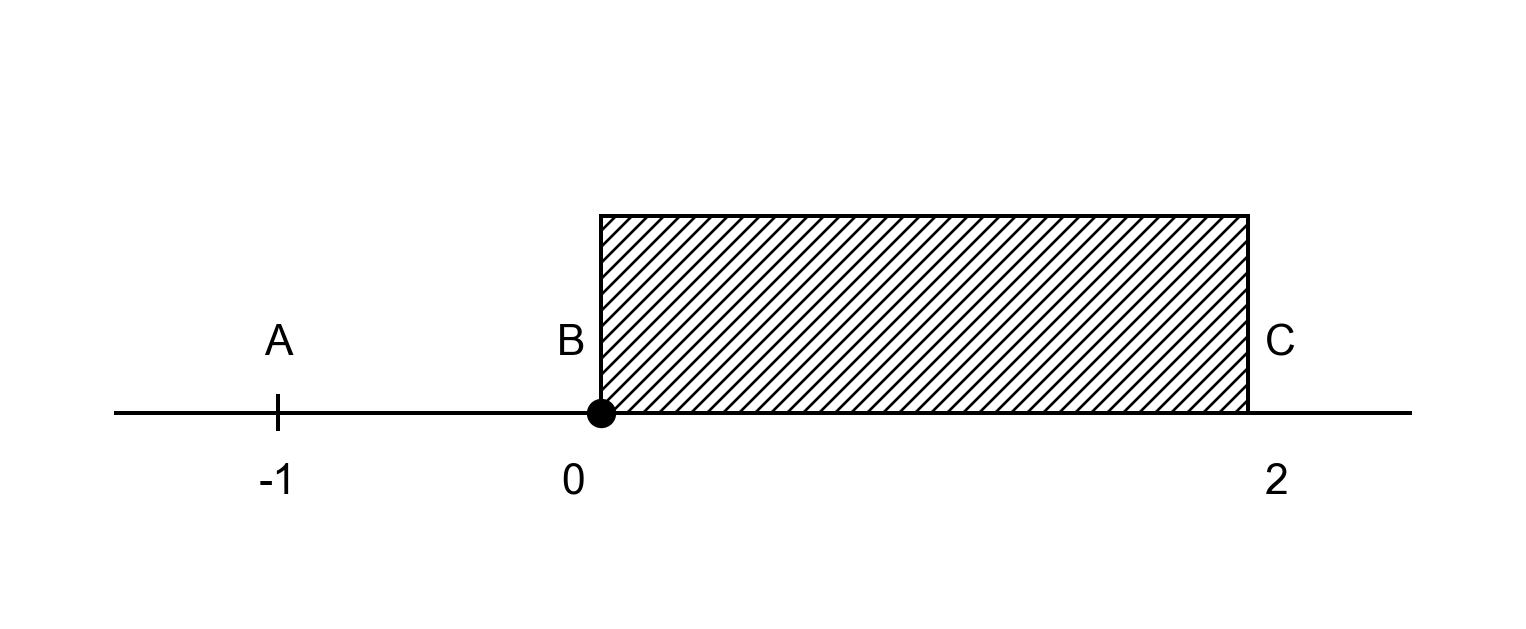
\(P\{X \ge 0\} = \frac{L_{BC}}{L_{AC}} = \frac{2}{3}\)
2-11. 指数分布 \(X \sim E(\lambda)\)
指数分布的概率密度: \[ f(x) = \begin{cases} \lambda e^{-\lambda x}, & x > 0, \\\\ 0, & x \le 0, \end{cases} \]
指数分布的分布函数 \[F(x) = \begin{cases} 1 - e^{-\lambda x}, & x \ge 0, \\\\ 0, & x < 0. \end{cases} \]
计算技巧:
当 \(a>0\) 且 \(X \sim E(\lambda)\) , \(P\{X>a\} = 1 - P\{X \le a\} = 1 - F(a) = e^{-\lambda a}\) ,当 \(a<=0\) 时,可以直接得出 \(P\{X>a\} = 1\) , 因为是必然事件
2-12. 正态分布 \(X \sim N(\sigma, \mu^2)\)
正态分布的概率密度: \[ f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}, -\infty < x < +\infty \]
\(Y = aX + b \sim N(a\mu + b, a^2\sigma^2), a \ne 0\) ,即正态随机变量的一次函数仍服从正态分布.
标准正态分布:
定义:当 \(\mu = 0, \sigma = 1\) 时,称 \(X\) 服从标准正态分布,记为 \(X \sim N(0,1)\),其概率密度为 \(\varphi(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}, -\infty < x < +\infty\),分布函数用 \(\Phi(x)\) 表示。
正态分布的标准化:
若 \(X \sim N(\mu, \sigma^2)\),则 \(Z = \frac{X-\mu}{\sigma} \sim N(0,1)\)。于是有
\(F(x) = P\{X \le x\} = P\{\frac{X-\mu}{\sigma} \le \frac{x-\mu}{\sigma}\} = \Phi(\frac{x-\mu}{\sigma})\)
\(P\{a < X \le b\} = P\{\frac{a-\mu}{\sigma} < \frac{X-\mu}{\sigma} \le \frac{b-\mu}{\sigma}\} = \Phi(\frac{b-\mu}{\sigma}) - \Phi(\frac{a-\mu}{\sigma})\)
标准正态分布的性质:
- \(\Phi(-a) = 1 - \Phi(a), \forall a \in R\);
- \(\Phi(0) = \frac{1}{2}\);
- \(P\{|X| \le a\} = 2\Phi(a) - 1\), 其中 \(a > 0\)
2-13. 随机变量函数 \(Y = g(X)\) 分布
这一节好好看看视频,要自己动手算,点击跳转到视频讲解链接
第三章-多维随机变量及其分布
%%{init: {
'flowchart': {
'curve': 'stepAfter',
'nodeSpacing': 20,
'rankSpacing': 50,
'padding': 10
}
}}%%
graph LR
classDef hidden fill:none,stroke:none,width:0px,height:0px
A3("多维随机变量及其分布")
P1[ ]:::hidden
A3 --- P1
P1 --> H1("二维离散型")
P1 --> H2("二维连续型")
P1 --> H3("联合分布函数")
P1 --> H4("独立性判别")
P1 --> H5("二维随机变量函数的分布")
P2[ ]:::hidden
H1 --- P2
P2 --> I1_1("求联合分布律")
P2 --> I1_2("求边缘分布律")
P2 --> I1_3("求条件分布律")
P2 --> I1_4("求概率")
P2 --> I1_5("已知条件分布求联合分布")
P2 --> I1_6("已知边缘分布和条件分布求联合分布")
P3[ ]:::hidden
H2 --- P3
P3 --> I2_1("已知联合概率密度")
P3 --> I2_2("已知联合分布函数")
P3 --> I2_3("利用充要条件")
P3 --> I2_4("求边缘概率密度")
P3 --> I2_5("求条件概率密度")
P3 --> I2_6("求概率")
P4[ ]:::hidden
I2_4 --- P4
P4 --> I2_7("求边缘概率密度")
P4 --> I2_8("求条件概率")
P3 --> J2_1("二维均匀分布")
P3 --> J2_2("二维正态分布")
P5[ ]:::hidden
H3 --- P5
P5 --> I3_1("已知联合分布律")
P5 --> I3_2("已知联合概率密度")
P5 --> I3_3("已知联合分布求边缘分布函数")
P6[ ]:::hidden
H4 --- P6
P6 --> I4_1("两个离散型")
P6 --> I4_2("两个连续型")
P6 --> I4_3("一个离散型一个连续型")
P7[ ]:::hidden
H5 --- P7
P7 --> I5_1("离散型 X Y")
P7 --> I5_2("连续型 X Y")
P7 --> I5_3("离散型X 和 连续型Y")
P7 --> I5_4("X Y 独立")
P7 --> I5_5("X Y 不独立")
P7 --> I5_6("正态分布且独立")
P7 --> I5_7("最大最小值分布")
P7 --> I5_8("常见可加性分布")
P8[ ]:::hidden
I5_2 --- P8
P8 --> J5_1("分布函数法")
P8 --> J5_2("公式法")
P8 --> J5_3("卷积公式法")
3-1. 多维随机变量及其分布函数
二维随机变量 \((X, Y)\) 的分布函数 \[ F(x, y) = P\{X \le x, Y \le y\} \] 它表示随机事件 \({X \le x} 和 {Y \le y}\) 同时发生的概率
将二维随机变量 \((X, Y)\) 看成是平面上随机点的坐标,那么,分布函数 \(F(x, y)\) 在点 \((x, y)\) 处的函数值就是随机点 \((X, Y)\) 落在为顶点而位于直线 \(X = x\) 的左侧和直线 \(Y = y\) 的下方的无穷矩形区域内的概率。 如下图:
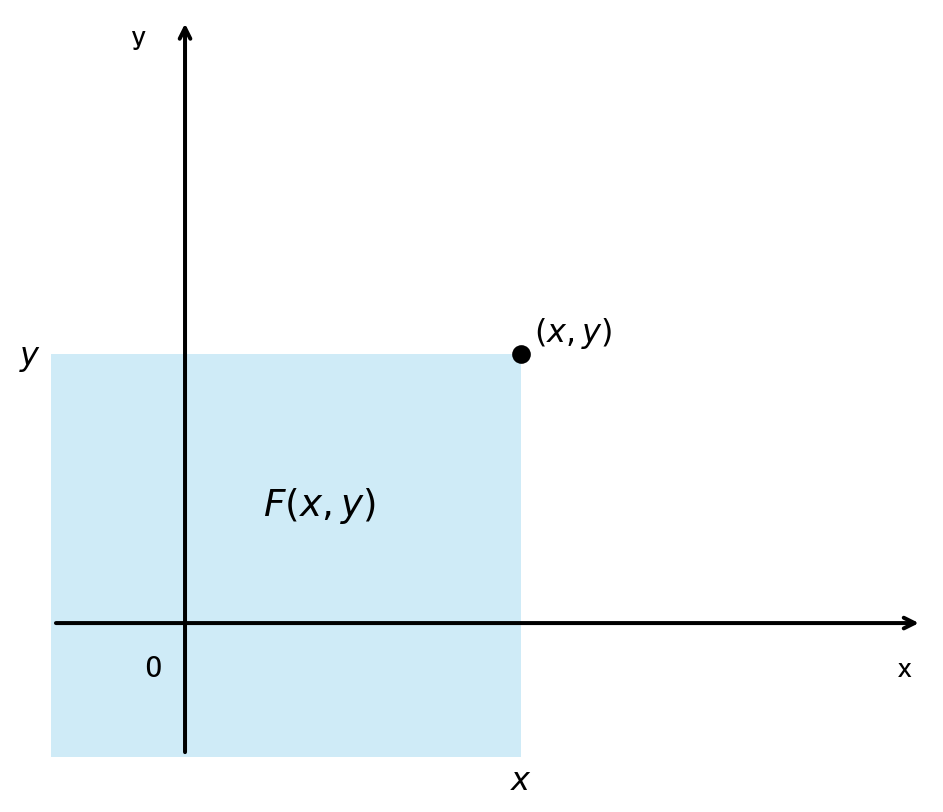
随机点 \((X, Y)\) 落在矩形区域 \(D = \{(x, y) | x_1 < X \le x_2, y_1 < Y \le y_2\}\) 内的概率为 \[ P\{x_1 < X \le x_2, y_1 < Y \le y_2\} = F(x_2, y_2) - F(x_1, y_2) - F(x_2, y_1) + F(x_1, y_1) \]
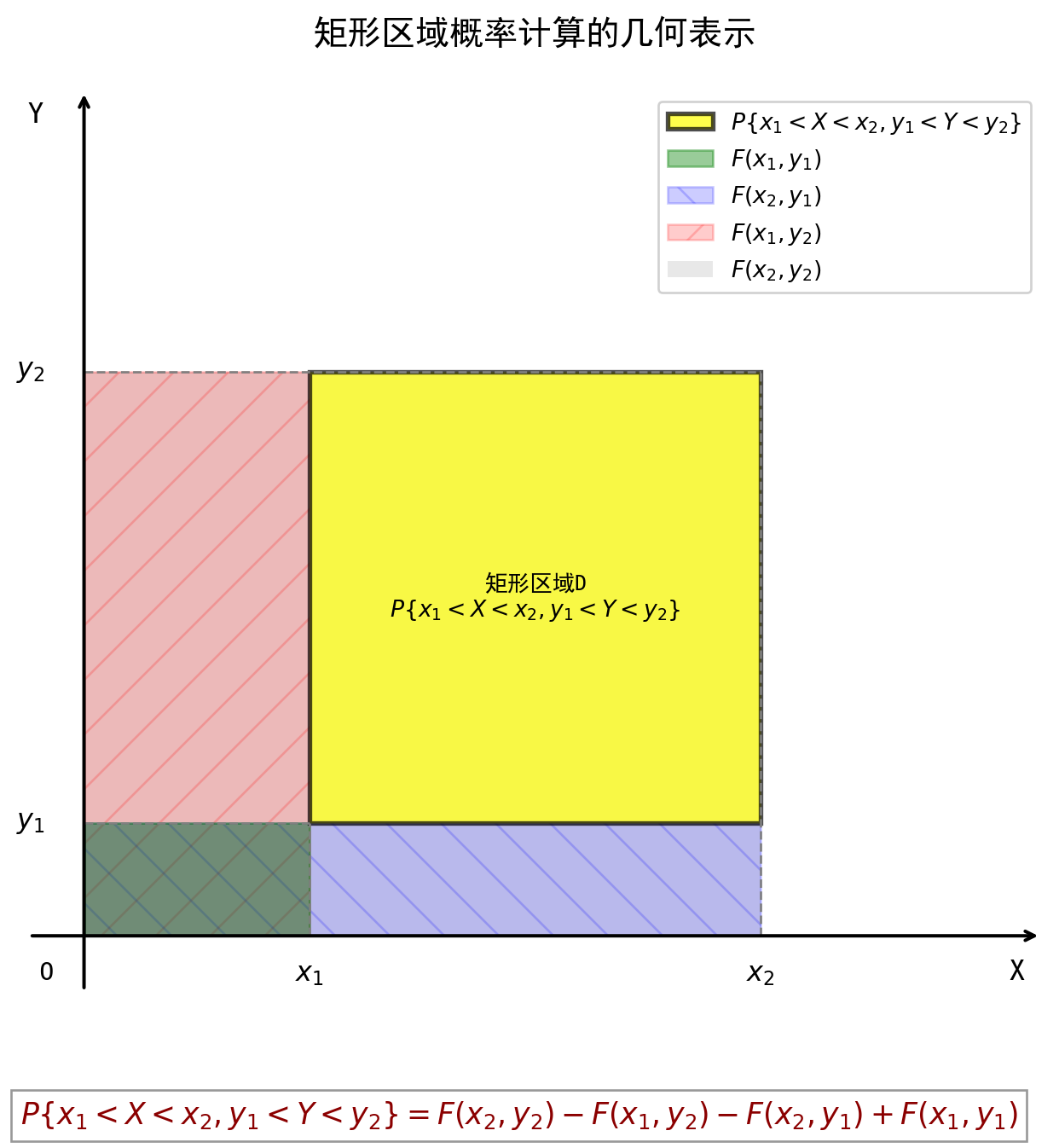
分布函数 \(F(X, Y)\) 的性质:
规范性:对于任意固定的 \(y\), \(F(-\infty, y) = \lim_{x \to -\infty} F(x, y) = 0\) ,对于任意固定的 \(x\), \(F(x, -\infty) = \lim_{y \to -\infty} F(x, y) = 0\), \(F(-\infty, -\infty) = 0\), \(F(+\infty, +\infty) = 1\) ,即 \(X\) 或者 \(Y\) 中只要有一个是负无穷,\(F(X,Y)\) 就为 \(0\) , 全为正无穷, \(F(X,Y)\) 才为1
单调不减性:\(F(x, y)\) 关于变量 \(x\) 和 \(y\) 单调不减,即对于任意固定的 \(y\),当 \(x_2 > x_1\) 时,\(F(x_2, y) \ge F(x_1, y)\);对于任意固定的 \(x\),当 \(y_2 > y_1\) 时,\(F(x, y_2) \ge F(x, y_1)\)
右连续性:\(F(x, y)\) 关于变量 \(x\) 右连续,关于 \(y\) 也右连续,即 \(F(x+0, y) = F(x, y), F(x, y+0) = F(x, y)\)
边缘分布函数:\(F_X(x) = P\{X \le x\} = P\{X \le x, Y < +\infty\} = F(x, +\infty)\),即 \(F_X(x) = F(x, +\infty)\),同理 \(F_Y(y) = F(+\infty, y)\)
如果 \(P\{X \le x, Y \le y\} = P\{X \le x\} \cdot P\{Y \le y\}\),即 \(F(x, y) = F_X(x) \cdot F_Y(y)\),则称随机变量 \(X\) 和 \(Y\) 相互独立。
性质: 设 \(X_1, X_2, ..., X_n\) 相互独立,且 \(g_1(x), g_2(x), ..., g_n(x)\) 均为连续函数,则 \(g_1(X_1), g_2(X_2), ..., g_n(X_n)\) 也相互独立.(独立随机变量的连续函数也独立)
比如:\(X和Y\) 独立,则 \(X^2\) 和 \(e^Y\) 也独立
3-2. 二维离散型随机变量的分布和独立性
二维离散型随机变量的分布律 \(P(X = x_i, Y = y_j) = p_{ij}, i, j = 1, 2, ...\) ,表示 \(X = x_i, Y = y_j\) 同时发生的概率是 \(p_{ij}\) , 由概率定义有 \(p_{ij} \ge 0, \sum_{i=1}^{+\infty} \sum_{j=1}^{+\infty} p_{ij} = 1\).
二维离散型随机变量的分布函数 \(F(x, y) = P\{X \le x, Y \le y\} = \sum_{x_i \le x} \sum_{y_j \le y} p_{ij}\)
\(X\) 的边缘分布律为: \[ P\{X = x_i\} = P\{X = x_i, Y < +\infty\} = \sum_{j=1}^{\infty} P\{X = x_i, Y = y_j\} = \sum_{j=1}^{\infty} p_{ij} = p_{i.}, i = 1, 2, ... \]
\(X\) 的边缘分布函数为: \[ F_X(x) = P\{X \le x\} = \sum_{x_i \le x} P\{X \le x_i\} = \sum_{x_i \le x} p_{i.} \]
同理,\(Y\) 的边缘分布律为:
\[ P\{Y = y_j\} = P\{X < +\infty, Y = y_j\} = \sum_{i=1}^{\infty} P\{X = x_i, Y = y_j\} = \sum_{i=1}^{\infty} p_{ij} = p_{.j}, j = 1, 2, ... \]
\(Y\) 的边缘分布函数为: \[ F_Y(x) = P\{Y \le y\} = \sum_{y_j \le y} P\{Y = y_j\} = \sum_{y_j \le y} p_{.j} \]
条件分布率定义: 设 \((x, Y)\) 是二维离散型随机变量,对于固定的 \(j\),若 \(P\{Y = y_j\} > 0\)
则称
\[ P\{X = x_i | Y = y_j\} = \frac{P\{X = x_i, Y = y_j\}}{P\{Y = y_j\}} = \frac{p_{ij}}{p_{.j}}, i = 1, 2, ... \]
为在 \(Y = y_j\) 条件下随机变量 \(X\) 的条件分布律。
下面作图直观演示下边缘分布函数计算过程
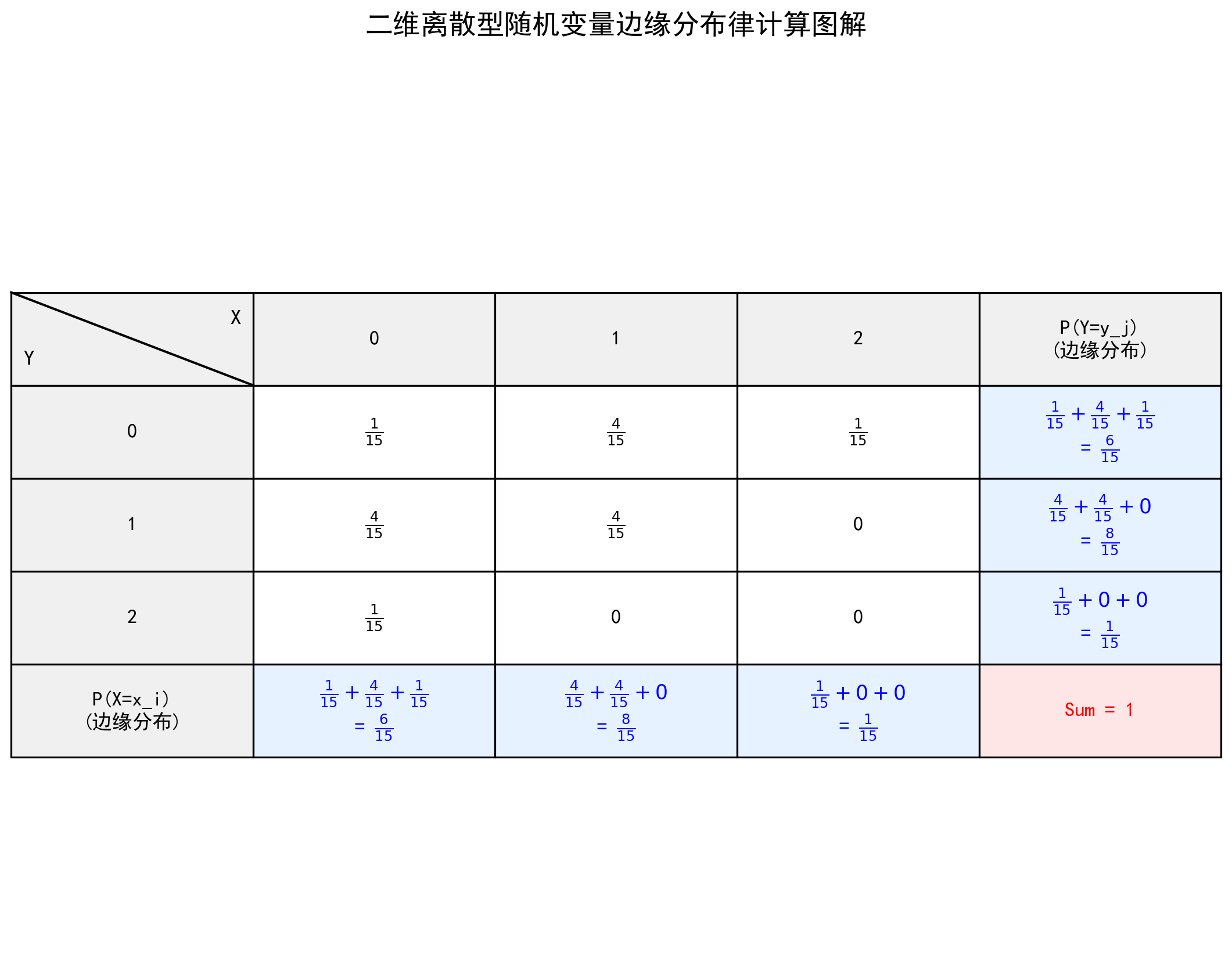
二维离散型随机变量 \(X\) 和 \(Y\) 独立的充要条件:
\(P\{X = x_i, Y = y_j\} = P\{X = x_i\} \cdot P\{Y = y_j\}, i, j = 1, 2, ...\)
即 \(p_{ij} = p_{i.} \cdot p_{.j}, (i, j = 1, 2, ...)\)
下面给出判断独立的小技巧:
如果有一个\(P\{X = x_i, Y = y_j\} = 0\) , 那么就可以直接判断不独立
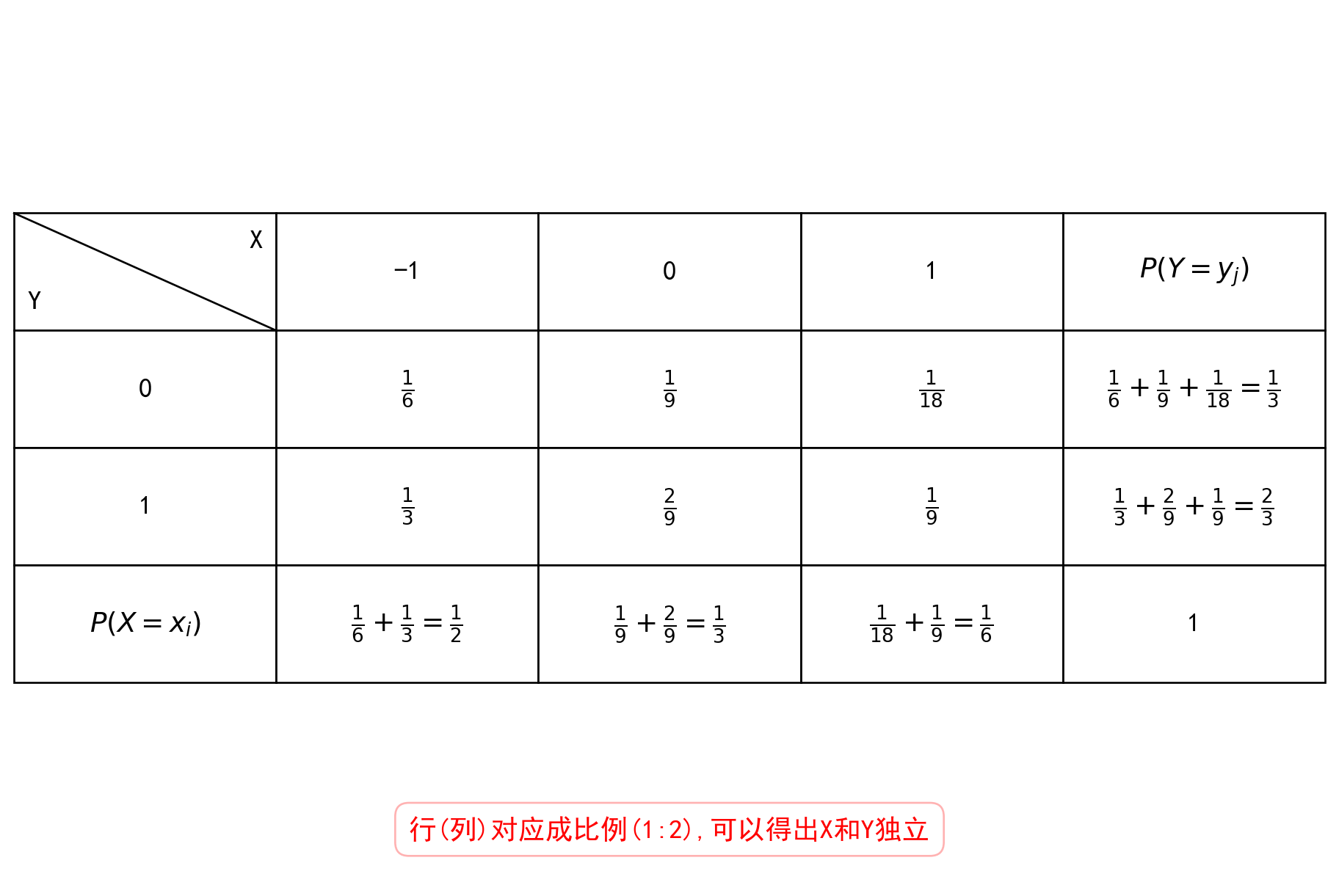
如果分布律表格中的行(列)对应成比例,那么一定独立
3-3. 二维连续型随机变量的概念和性质
和一维概率密度函数 \(f(x)\) 的一样,二维连续型随机变量的概率密度函数 \(f(x,y)\) 同样也是 \(X\) 和 \(Y\) 都是连续型随机变量才存在
二维连续型随机变量的分布函数: \[ F(x, y) = P\{X \le x, Y \le y\} = \int_{-\infty}^{x} \int_{-\infty}^{y} f(u, v) du dv \]
联合密度函数性质: \[\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(x, y) dxdy = 1 \]
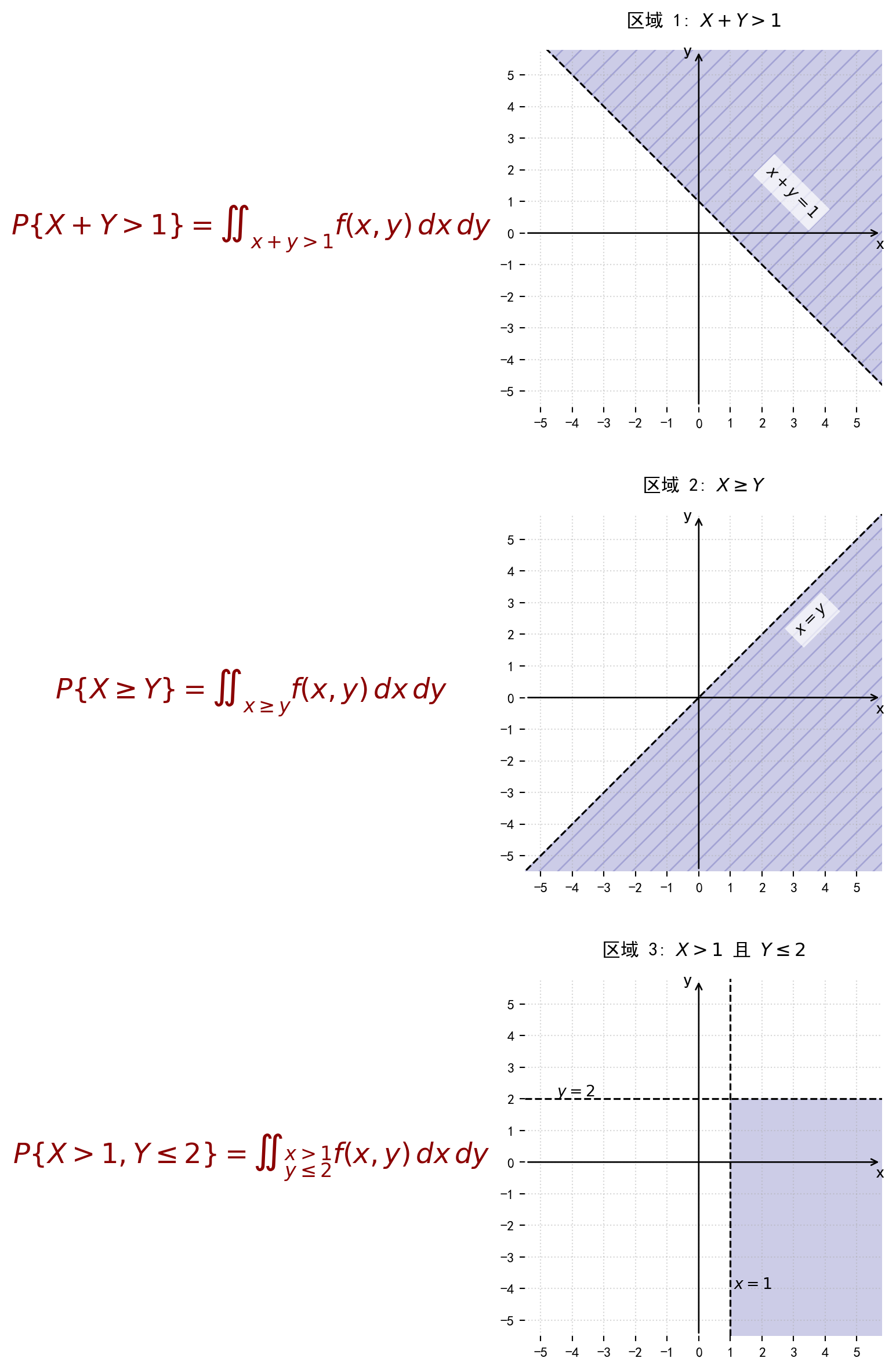
设 \(G\) 是 \(xOy\) 平面上任一区域,则点 \((X, Y)\) 落在 \(G\) 内的概率为
\[ P\{(X, Y) \in G\} = \iint_{G} f(x, y) dxdy \]
若 \(f(x, y)\) 在点 \((x, y)\) 处连续,则有 \(f(x, y) = \frac{\partial^2 F(x,y)}{\partial x \partial y}\). 如果给出了 \(F(x,y)\) 一般情况下,\(F(x,y)\) 是连续的,那么可以直接求二阶偏导得到 \(f(x,y)\)
3-4. 二维连续型随机变量求概率和分布函数
设二维随机变量 \((X,Y)\) 的密度函数为
\(f(x,y) = \begin{cases} Cxy, & 0 \le x \le 1, 0 \le y \le 1, \\ 0, & \text{其他}. \end{cases}\)
求: (I) 常数 \(C\); (II) \(P\{X+Y < 1\}\); (III) 联合分布函数 \(F(x,y)\).
(I)点击查看答案4
(II)点击查看答案 \(\frac{1}{6}\)
(III)点击查看答案\[F(x,y) = \begin{cases} 0, & x<0 \text{ 或 } y<0 \\ x^2y^2, & 0 \le x < 1, 0 \le y < 1 \\ x^2, & 0 \le x < 1, y \ge 1 \\ y^2, & 0 \le y < 1, x \ge 1 \\ 1, & x \ge 1, y \ge 1 \end{cases}\]
3-5. 边缘概率密度
\(X\) 的边缘分布函数 \(F_X(x) = F(x, +\infty) = \int_{-\infty}^{x} [\int_{-\infty}^{+\infty} f(x, y) dy] dx\),其密度函数为 \(f_X(x) = F'_X(x) = \int_{-\infty}^{+\infty} f(x, y) dy\)
同理,\(Y\) 的边缘分布函数为 \(F_Y(y) = F(+\infty, y) = \int_{-\infty}^{y} [\int_{-\infty}^{+\infty} f(x, y) dx] dy\),其密度函数为 \(f_Y(y) = F'_Y(y) = \int_{-\infty}^{+\infty} f(x, y) dx\),分别称 \(f_X(x)\) 和 \(f_Y(y)\) 为 \((X, Y)\) 关于 \(X\) 和 \(Y\) 的边缘概率密度。
3-6. 条件概率密度与条件概率
设二维随机变量 \((X, Y)\) 的概率密度为 \(f(x, y)\). 若对于固定的 \(y\), \(f_Y(y) > 0\) 则称 \[ f_{X|Y}(x|y) = \frac{f(x, y)}{f_Y(y)} \] 为在 \(Y = y\) 的条件下 \(X\) 的条件概率密度
若对于固定的 \(x\), \(f_X(x) > 0\), 则称 \[ f_{Y|X}(y|x) = \frac{f(x, y)}{f_X(x)} \] 为在 \(X = x\) 的条件下 \(Y\) 的条件概率密度
\[ P\{X \le x | Y = y\} = \int_{-\infty}^{x} f_{X|Y}(u|y) du \]
辨析:\(P\{X \le x | Y = y\}\) 和 \(P\{X \le x | Y > y\}\)
前者是条件概率密度,后者是条件概率
计算 \(P\{X \le x | Y = y\}\) 的步骤:
先求边缘密度:\(f_Y(y) = \int_{-\infty}^{+\infty} f(x,y) dx\)。
再求条件密度:\(f_{X|Y}(x|y) = \frac{f(x,y)}{f_Y(y)}\)
最后积分:\(P\{X \le x | Y = y\} = \int_{-\infty}^{x} f_{X|Y}(u|y) du\)
计算 \(P\{X \le x | Y > y\}\) 的步骤:
\[ P\{X \le x | Y > y\} = \frac{P(X \le x, Y > y)}{P(Y > y)} \]
注意书写规范,在写条件概率密度函数的时候,一定要先注明:在 \(X = x(x的范围) or Y = y(y的范围)\) 的条件下,\(f_{Y|x}(y|x) = ...\) or \(f_{X|Y}(x|y) = ...\)
3-7. 二维连续型随机变量的独立性
对于二维连续型随机变量 \((X, Y)\),则 \(X\) 与 \(Y\) 相互独立的充要条件是 \[f(x, y) = f_X(x) \cdot f_Y(y)\]
判读二维连续型随机变量的独立性的小技巧: 1. \(f(x,y)\) 的表达式中,可以拆成 \(g(x) \cdot h(y)\) 2. \(x\) 和 \(y\) 的范围互不影响,各自写各自的 只有同时满足条件1和2时,才能说 \(X\) 和 \(Y\) 独立
eg: \[f(x, y) = \begin{cases} \frac{1}{2}e^{-\frac{y}{2}}, & 0 < x < 1, y > 0 \\ 0, & \text{其他} \end{cases}\] 这里可以很明显的看出 \(f(x, y)\) 是变量可分离的,并且 \(x\) 和 \(y\) 的取值范围都不相干
\[f(x, y) = \begin{cases} 3e^{-(x+3y)}, & x > 0, y > 0, \\ 0, & \text{其他}, \end{cases}\] 同样的,\(3e^{-(x+3y)}\) 也可以拆成 \(g(x) \cdot h(y)\) 的形式并且 \(x\) 和 \(y\) 的取值范围都不相干
\[f(x, y) = \begin{cases} (x+1)(y+1), & 0 < x < 1, 0 < y < 1-x \\ 0, & \text{其他} \end{cases}\] 这个就不独立了,因为\(x\) 和 \(y\) 的取值范围有联系
3-8. 二维连续型随机变量综合题(练习)
设二维随机变量 \((X,Y)\) 具有概率密度
\[f(x,y) = \begin{cases} Ae^{-(x+y)}, & 0 < x < y \\ 0, & \text{其他} \end{cases}\]
试求:(1) 常数 \(A\); (2) \(P\{X+Y > 1, X < \frac{1}{2}\}\); (3) \(X,Y\) 的边缘概率密度 \(f_X(x), f_Y(y)\); (4) 条件概率密度 \(f_{Y|X}(y|x)\); (5) \(X\) 与 \(Y\) 是否独立?
3-9. 二维均匀分布
\[ f(x, y) = \begin{cases} \frac{1}{S_D}, & (x, y) \in D, \\ 0, & \text{其他}, \end{cases} \]
性质:若 \((X, Y)\) 在 \(D\) 上服从二维均匀分布,则对 \(D\) 内的任意子区域 \(G\),有 \[P\{(X, Y) \in G\} = \frac{S_G}{S_D}\]
3-10. 二维正态分布
定义 若二维随机变量 \((X,Y)\) 的概率密度为
\[ f(x, y) = \frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}} \exp\left\{-\frac{1}{2(1-\rho^2)} \left[\frac{(x-\mu_1)^2}{\sigma_1^2} - 2\rho\frac{x-\mu_1}{\sigma_1}\frac{y-\mu_2}{\sigma_2} + \frac{(y-\mu_2)^2}{\sigma_2^2}\right]\right\} \]
\((x, y) \in R^2\), 其中参数 \(\mu_1, \mu_2, \sigma_1, \sigma_2, \rho\) 均为常数,且 \(\sigma_1 > 0, \sigma_2 > 0, |\rho| < 1\), 则称 \((X,Y)\) 服从参数为 \(\mu_1, \mu_2, \sigma_1, \sigma_2\) 和 \(\rho\) 的二维正态分布,记作 \((X,Y) \sim N(\mu_1, \mu_2; \sigma_1^2, \sigma_2^2; \rho)\).
\(f(x,y)\) 的表达式太复杂了,不用背,了解即可
性质:
边缘分布是正态分布, 即 \(X \sim N(\mu_1, \sigma_1^2), Y \sim N(\mu_2, \sigma_2^2)\)
\(X\) 与 \(Y\) 相互独立的充要条件为 \(\rho = 0\)
\(X\) 与 \(Y\) 的非零线性组合 \(aX + bY\) 仍服从正态分布, 且 \(aX + bY \sim N(a\mu_1 + b\mu_2, a^2\sigma_1^2 + b^2\sigma_2^2 + 2ab\rho\sigma_1\sigma_2)\).
条件分布是正态分布
3-11. 二维随机变量函数分布(离散型)
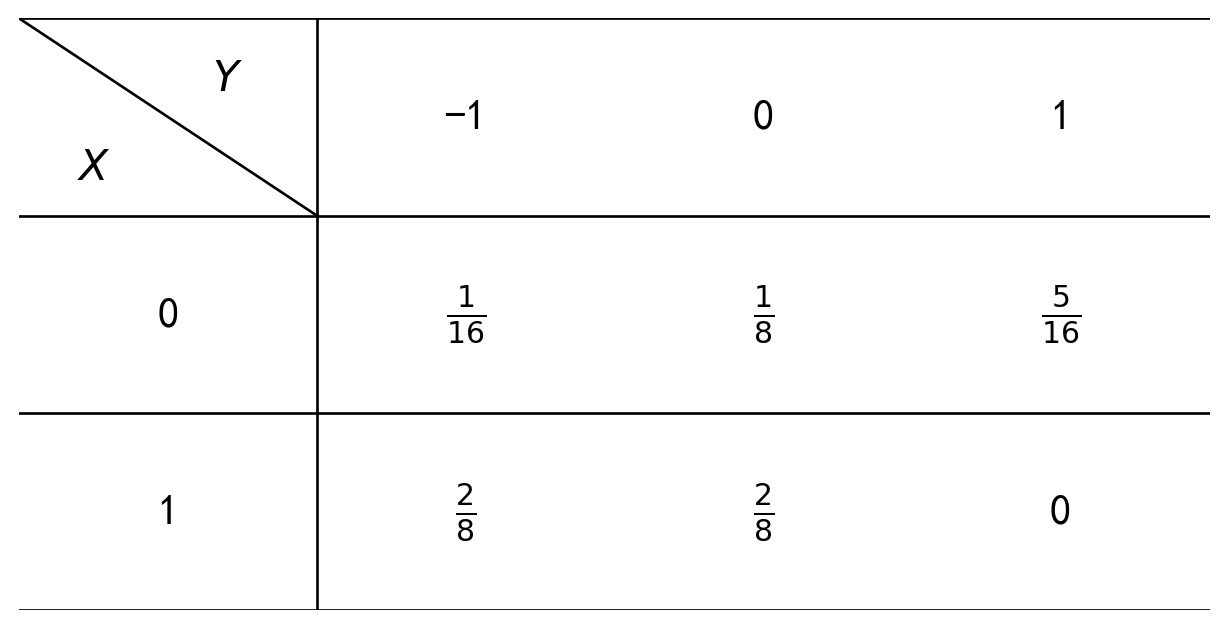
- 求 \(U = X + Y\) 的概率分布. (2) 求 \(V = \min(X, Y)\) 的概率分布
3-12. 二维随机变量函数分布(连续型)
分布函数法:
分布函数 \[ F_Z(z) = P\{Z \le z\} = P\{g(X, Y) \le z\} = \iint_{g(x, y) \le z} f(x, y) dxdy \] 将 \(z\) 取遍 \((-\infty, +\infty)\), 计算二重积分得 \(F_Z(z)\) 的函数表达式.
公式法:
设 \((X, Y)\) 的概率密度为 \(f(x, y)\),则若 \(Z = g(X, Y)\) 可反解得 \(Y = h(X, Z)\),则 \[f_Z(z) = \int_{-\infty}^{+\infty} \left|\frac{\partial h(x, z)}{\partial z}\right| f(x, h(x, z)) dx\]
同理,若 \(Z = g(X, Y)\) 可反解得 \(X = \varphi(Y, Z)\),则 \[f_Z(z) = \int_{-\infty}^{+\infty} \left|\frac{\partial \varphi(y, z)}{\partial z}\right| f(\varphi(y, z), y) dy\]
分布函数法是通法,但计算量一般来讲比较大,公式法只有在能反解到X或Y的时候才能用,计算量一般比分布函数法小,考试的题目一般都能用公式法
3-13. 二维随机变量函数分布(正态)
当 \(X\) 和 \(Y\) 均服从正态分布且相互独立, \(X \sim N(\mu_1, \sigma_1^2)\), \(Y \sim N(\mu_2, \sigma_2^2)\), \(Z = aX + bY\),可以直接得到
已知 \(Z \sim N(a\mu_1 + b\mu_2, a^2\sigma_1^2 + b^2\sigma_2^2)\),其概率密度函数 \(f(z)\) 为:
\[ \begin{aligned} f(z) = \frac{1}{\sqrt{2\pi(a^2\sigma_1^2 + b^2\sigma_2^2)}} \exp \left\{ -\frac{[z - (a\mu_1 + b\mu_2)]^2}{2(a^2\sigma_1^2 + b^2\sigma_2^2)} \right\} \end{aligned} \]
3-14. 最大最小值分布
设 \(X_1, X_2, ..., X_n\) 是相互独立的随机变量,分布函数分别为 \(F_{X_1}(x), F_{X_2}(x), ..., F_{X_n}(x)\),则 \(U = \max(X_1, X_2, ..., X_n)\) 的分布函数为
\[ F_{\max}(z) = F_{X_1}(z)F_{X_2}(z)...F_{X_n}(z) \]
推导过程:
\(U = \max\{X_1, ..., X_n\}\)
\[ \begin{aligned} F_U(z) &= P\{U \le z\} = P\{\max\{X_1, X_2, \dots, X_n\} \le z\} \\ &= P\{X_1 \le z, X_2 \le z, \dots, X_n \le z\} \\ &= P\{X_1 \le z\}P\{X_2 \le z\} \dots P\{X_n \le z\} \\ &= F_{X_1}(z) F_{X_2}(z) \dots F_{X_n}(z) \end{aligned} \]
\(V = \min(X_1, X_2, ..., X_n)\) 的分布函数为
\[ F_{\min}(z) = 1 - [1 - F_{X_1}(z)][1 - F_{X_2}(z)]...[1 - F_{X_n}(z)] \]
特别地,当 \(X_1, X_2, ..., X_n\) 相互独立且 \(X_i \sim F(x)\) 时有:
\[ F_{\max}(z) = [F(z)]^n, F_{\min}(z) = 1 - [1 - F(z)]^n \]
推导过程:
\[ \begin{aligned} F_V(z) &= P\{\min\{X_1, X_2, \dots, X_n\} \le z\} \\ &= 1 - P\{\min\{X_1, X_2, \dots, X_n\} > z\} \\ &= 1 - P\{X_1 > z, X_2 > z, \dots, X_n > z\} \\ &= 1 - P\{X_1 > z\}P\{X_2 > z\} \dots P\{X_n > z\} \\ &= 1 - [1 - F_{X_1}(z)][1 - F_{X_2}(z)] \dots [1 - F_{X_n}(z)] \end{aligned} \]
第四章-数字特征
%%{init: {'flowchart': {'curve': 'stepAfter'}}}%%
graph LR
classDef hidden fill:none,stroke:none,width:0px,height:0px
A1(数字特征)
N1[ ]:::hidden
A1 --- N1
N1 --> B1("求数学期望、方差")
N1 --> B2(求协方差与相关系数)
N2[ ]:::hidden
B1 --- N2
N2 --> C1(一维)
N2 --> C2(二维)
N2 --> C3(运算性质)
N2 --> C4(常用分布的期望和方差)
N3[ ]:::hidden
C1 --- N3
N3 --> D1(离散型X及其函数)
N3 --> D2(连续型X及其函数)
N4[ ]:::hidden
C2 --- N4
N4 --> D3("离散型 (X, Y) 及其函数")
N4 --> D4("连续型 (X, Y) 及其函数")
N4 --> D5("max {X, Y}, min {X, Y} 的期望")
N5[ ]:::hidden
B2 --- N5
N5 --> D6(判别X和Y是否相关)
4-1. 数学期望
离散型数学期望:
若级数 \(\sum_{k=1}^{\infty} x_k p_k\) 绝对收敛,则称该级数为 \(X\) 的数学期望,记为 \(EX\) \[ EX = \sum_{k=1}^{\infty} x_k p_k \] 否则,则 \(X\) 的数学期望不存在
连续型数学期望:
若 \(\int_{-\infty}^{+\infty} |x| f(x) dx < +\infty\) ,则称 \[ EX = \int_{-\infty}^{+\infty} x f(x) dx \] 为 \(X\) 的数学期望,否则,则 \(X\) 的数学期望不存在
一维随机变量的函数 \(Y = g(X)\) 的期望:
离散型: \[ EY = E[g(X)] = \sum_{k=1}^{\infty} g(x_k) p_k \]
连续型: \[ EY = E[g(X)] = \int_{-\infty}^{+\infty} g(x) f(x) dx \]
数学期望的性质:
\(E(C) = C\) (其中 \(C\) 为常数)
\(E(X + C) = E(X) + C\)
\(E(CX) = CE(X)\)
\(E(X \pm Y) = E(X) \pm E(Y)\)
设 \(X, Y\) 相互独立,则 \(E(XY) = EXEY\)
4-2. 二维随机变量函数的期望
二维随机变量函数 \(Z = g(X,Y)\) 的期望
离散型:
\[ EZ = E[g(X, Y)] = \sum_{j=1}^{\infty} \sum_{i=1}^{\infty} g(x_i, y_i) p_j \]
连续型:
\[ EZ = E[g(X, Y)] = \iint_{-\infty}^{+\infty} g(x, y) f(x, y) dxdy \]
4-3. 方差
定义: 设 \(X\) 为一随机变量,若 \(E(X - EX)^2\) 存在,则称 \(E(X - EX)^2\) 为 \(X\) 的方差,记为 \(DX\),即
\(DX = E(X - EX)^2\)
称 \(\sqrt{DX}\) 为 \(X\) 的标准差. 易得计算公式 \(DX = EX^2 - (EX)^2\). 显然 \(DX \ge 0\).
计算时,\(DX = EX^2 - (EX)^2\) 这个公式用的最多
方差的性质:
\(D(C) = 0\) (其中 \(C\) 为常数);
\(D(X + C) = DX\)
\(D(CX) = C^2DX\)
设 \(X, Y\) 相互独立,则 \(D(X \pm Y) = DX + DY\)(这里注意和期望的性质区分,\(E(X \pm Y) = E(X) \pm E(Y)\) 是通用的,不管 \(X 和 Y\) 是否独立)
\(DX = 0\) 的充要条件是 \(P\{X = EX\} = 1\)
4-4. 常见分布的期望和方差
| 分布类型 | 分布律或概率密度 | 期望 | 方差 |
|---|---|---|---|
| 0-1 分布 | \(p_k = P\{X=k\} = p^k q^{1-k} \quad (q=1-p), (k=0,1)\) | \(p\) | \(pq\) |
| 二项分布 | \(p_k = P\{X=k\} = C_n^k p^k q^{n-k}\) \((q=1-p), (k=0,1,\dots,n)\) |
\(np\) | \(npq\) |
| 泊松分布 | \(p_k = P\{X=k\} = \frac{\lambda^k}{k!} e^{-\lambda} \quad (k=0,1,2\dots)\) | \(\lambda\) | \(\lambda\) |
| 均匀分布 | \(f(x) = \begin{cases} \frac{1}{b-a}, & a < x < b \\ 0, & \text{其他} \end{cases}\) | \(\frac{a+b}{2}\) | \(\frac{(b-a)^2}{12}\) |
| 正态分布 | \(f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \quad (-\infty < x < +\infty, \sigma > 0)\) | \(\mu\) | \(\sigma^2\) |
| 指数分布 | \(f(x) = \begin{cases} \lambda e^{-\lambda x}, & x > 0 \\ 0, & x \le 0 \end{cases}\) | \(\frac{1}{\lambda}\) | \(\frac{1}{\lambda^2}\) |
| \(\chi^2\) 分布 | \(X_1, X_2, \dots, X_n\) 相互独立,且都服从标准正态分布 \(N(0,1)\) \(\chi^2 = X_1^2 + X_2^2 + \dots + X_n^2\) |
\(n\) | \(2n\) |
| 几何分布 | \(p_k = P\{X=k\} = (1-p)^{k-1} p\) \((k=1,2,\dots), 0 < p < 1\) |
\(\frac{1}{p}\) | \(\frac{1-p}{p^2}\) |
记住后做题直接用
4-5. 最大最小值分布的期望
回顾一下最大值最小值分布:
\[F_{\max}(z) = F_{X_1}(z)F_{X_2}(z)...F_{X_n}(z)\]
\[F_{\min}(z) = 1 - [1 - F_{X_1}(z)][1 - F_{X_2}(z)]...[1 - F_{X_n}(z)]\]
设随机变量 \(X\) 与 \(Y\) 相互独立,且都服从参数为 1 的指数分布,记 \(U = \max\{X, Y\}, V = \min\{X, Y\}\),求 (I) \(EU\); (II) \(EV\); (III) \(EUV\)
结论:\(U + V = X + Y\), \(UV = XY\), \(U - V = |X - Y|\)
4-6. 切比雪夫不等式
定义:设随机变量具有数学期望 \(EX = \mu\),方差 \(DX = \sigma^2\),则对于任意正数 \(\epsilon\),有下列切比雪夫不等式成立
\(P\{|X - EX| \ge \epsilon\} \le \frac{DX}{\epsilon^2}\) 或 \(P\{|X - EX| < \epsilon\} \ge 1 - \frac{DX}{\epsilon^2}\)
注意,这里只需要随机变量的数学期望和方差存在即可,并不需要该随机变量是正态随机变量
4-7. 协方差
定义:对于二维随机变量 \((X, Y)\),若 \(E(X - EX)(Y - EY)\) 存在,则称它为 \(X\) 与 \(Y\) 的协方差,记为 \(Cov(X, Y)\),即
\[ Cov(X, Y) = E(X - EX)(Y - EY) \]
易得计算公式 \[ Cov(X, Y) = EXY - EXEY \]
性质:
\(Cov(X, Y) = Cov(Y, X)\);
\(Cov(X, C) = 0\);
\(Cov(aX, bY) = abCov(X, Y)\);
\(Cov(X, X) = DX\)
设 \(X, Y\) 相互独立, 则 \(Cov(X, Y) = 0\)
\(D(X \pm Y) = DX + DY \pm 2Cov(X, Y)\).
\(Cov(X \pm Y, Z) = Cov(X, Z) \pm Cov(Y, Z)\);
性质1-5都可以由 \(Cov(X, Y) = EXY - EXEY\) 推出来
性质7可以用乘法分配律来理解,把协方差 \(Cov((a \pm b),c)\) 看作一种特殊的“乘法”, \((a \pm b)×c=ac \pm bc\)
举个例子来加深对以上性质的理解
设 \(X_1, X_2, X_3 \stackrel{iid}{\sim} N(0, 9) 且Cov(X_1 + 2X_2 - 3X_3, 2X_3 + 5)\)
题目要求计算 \(Cov(X_1 + 2X_2 - 3X_3, 2X_3 + 5)\),推导步骤如下:
\[ \begin{aligned} &Cov(X_1 + 2X_2 - 3X_3, 2X_3 + 5) \\ = \ &Cov(X_1 + 2X_2 - 3X_3, 2X_3) && \text{(由性质2:} Cov(X, C) = 0 \text{)} \\ = \ &Cov(- 3X_3, 2X_3) && \text{(由性质5:变量相互独立则协方差为 0)} \\ = \ &-6 Cov(X_3, X_3) && \text{(由性质3:} Cov(aX, bY) = ab Cov(X, Y) \text{)} \\ = \ &-6 DX_3 && \text{(由性质4:} Cov(X, X) = DX \text{)} \\ = \ &-6 \times 9 = -54 \end{aligned} \]
结论:最终结果为 -54
例题:设随机变量 \((X, Y)\) 的密度函数 \(f(x, y) = \begin{cases} 3, & (x, y) \in G \\ 0, & \text{其他} \end{cases}\),其中区域 \(G\) 由曲线 \(y = x^2\) 与 \(x = y^2\) 围成. 求 \(Cov(X, Y)\)
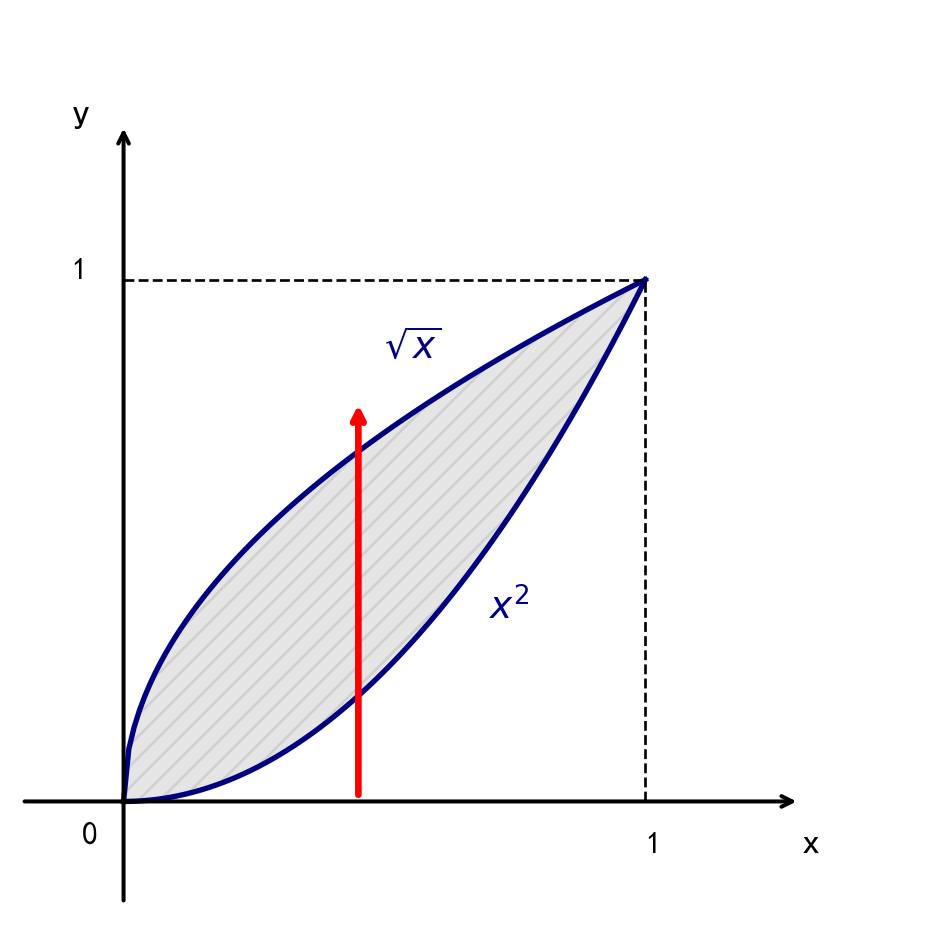
首先列出核心公式: \[Cov(X,Y) = EXY - EX \cdot EY\]
第一步:计算混合矩 \(EXY\) \[ \begin{aligned} EXY &= \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} xy f(x, y) \, dx \, dy \\ &= \int_{0}^{1} 3x \, dx \int_{x^2}^{\sqrt{x}} y \, dy \\ &= \frac{1}{4} \end{aligned} \]
技巧点拨:计算 \(EX\) 时,不必先求边缘分布 \(f_X(x)\),直接利用二维期望公式 \(EX = \iint x f(x,y) \, dx \, dy\) 更快。
第二步:计算边缘矩 \(EX\) \[ \begin{aligned} EX &= \int_{0}^{1} 3x \, dx \int_{x^2}^{\sqrt{x}} dy \\ &= \int_{0}^{1} 3x (\sqrt{x} - x^2) \, dx \\ &= \frac{9}{20} \end{aligned} \]
由区域和密度的对称性可知:\(EY = EX = \frac{9}{20}\)
最后计算协方差 \(Cov(X,Y)\): \[ \begin{aligned} Cov(X,Y) &= EXY - EX \cdot EY \\ &= \frac{1}{4} - \left( \frac{9}{20} \right) \cdot \left( \frac{9}{20} \right) \\ &= \frac{100}{400} - \frac{81}{400} \\ &= \frac{19}{400} \end{aligned} \]
4-8. 相关系数
定义对于二维随机变量 \((X, Y)\),若 \(DX \ne 0, DY \ne 0\),则称 \[ \rho_{XY} = \frac{Cov(X, Y)}{\sqrt{DX} \cdot \sqrt{DY}} \] 为 \(X\) 和 \(Y\) 的相关系数. 若 \(\rho_{XY} = 0\),称 \(X\) 和 \(Y\) 不相关.
性质
- \(|\rho_{XY}| \le 1, \rho_{XY} = \rho_{YX}, \rho_{XX} = 1\);
- \(|\rho_{XY}| = 1\) 的充要条件是 \(X\) 与 \(Y\) 以概率 1 线性相关,即存在常数 \(a \ne 0\) 和 \(b\), 有 \(P\{Y = aX + b\} = 1\)
- \(|\rho_{XY}|\) 越接近于 1,表明 \(X\) 和 \(Y\) 的线性相关程度越大
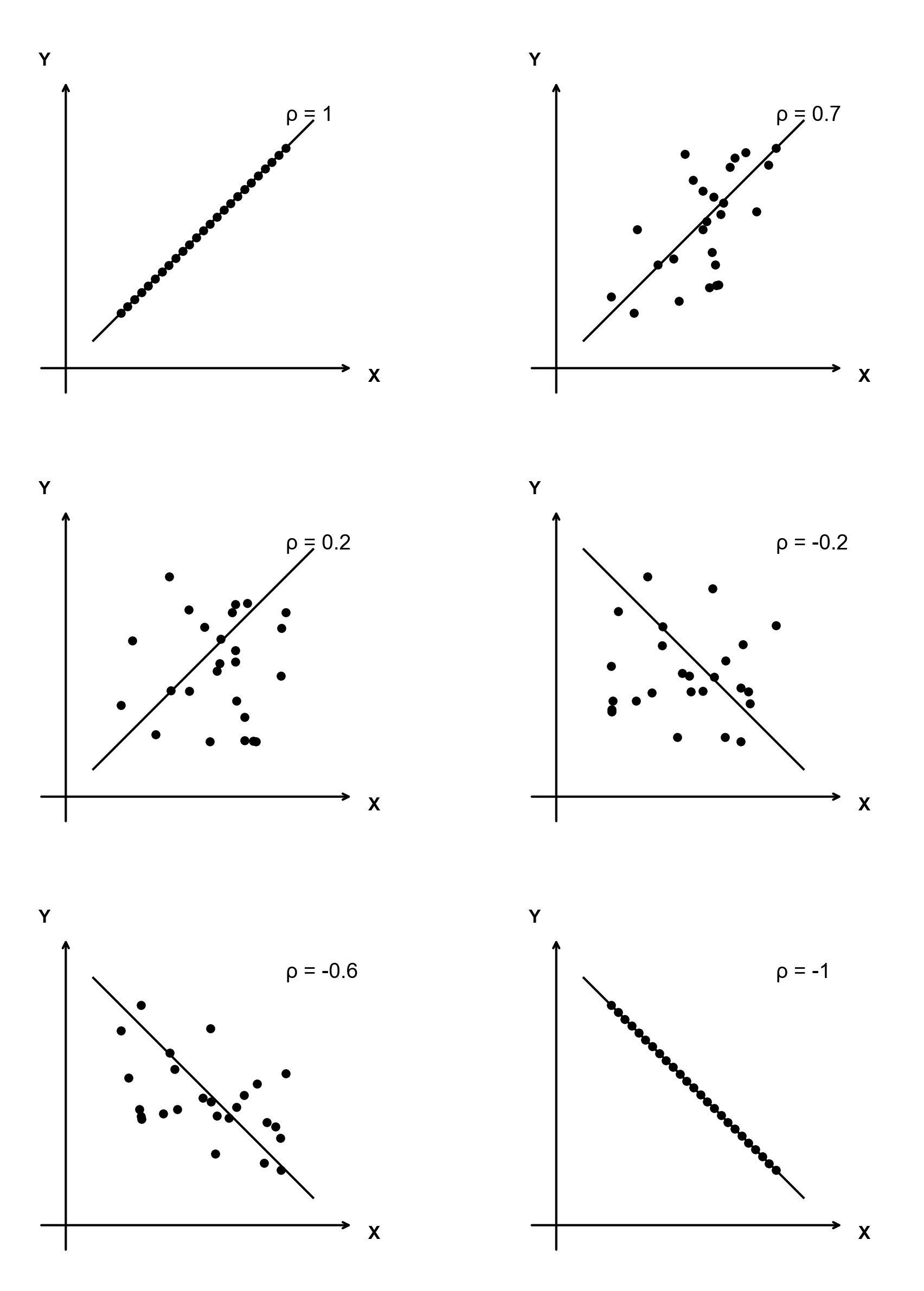
易错:\(Y=-X+3\) 的相关系数是 \(-1\). \(Y = -\frac{1}{2}X+3\) 的相关系数也是-1而不是 \(-\frac{1}{2}\)
其实,可以证明:只要有 \(Y = aX + b\),那么一定有 \[ \rho_{XY} = \begin{cases} 1, & a > 0 \\ -1, & a < 0 \end{cases} \]
4-9. 不相关与独立
常用结论:
- 任意随机变量 \(X\) 与 \(Y\) 相互独立是 \(X\) 与 \(Y\) 不相关的充分不必要条件.(独立可以推出不相关,但不相关不能推出独立)
- 对随机变量 \(X, Y\), 有下列等价命题: \[ \rho_{XY} = 0 \Leftrightarrow Cov(X, Y) = 0 \Leftrightarrow EXY = EXEY \Leftrightarrow D(X \pm Y) = DX + DY \]
第五章-大数定理和中心极限定理
%%{init: {'flowchart': {'curve': 'stepAfter'}}}%%
graph LR
classDef hidden fill:none,stroke:none,width:0px,height:0px
A1("大数定律和中心极限定理")
N1[ ]:::hidden
A1 --- N1
N1 --> B1(大数定律)
N1 --> B2(中心极限定理)
N2[ ]:::hidden
B1 --- N2
N2 --> C1(依概率收敛)
N2 --> C2(切比雪夫大数定律)
N2 --> C3(辛钦大数定律)
N2 --> C4(伯努利大数定律)
N3[ ]:::hidden
B2 --- N3
N3 --> C5(列维-林德伯格定理)
N3 --> C6(棣莫弗-拉普拉斯定理)
5-1. 依概率收敛与大数定律
依概率收敛定义:
设 \(\{X_n\}\) 是一随机变量序列, \(a\) 是常数, 若对任意 \(\varepsilon > 0\), 有
\[ \lim_{n \to \infty} P\{|X_n - a| \ge \varepsilon\} = 0 \]
或等价地有 \[ \lim_{n \to \infty} P\{|X_n - a| < \varepsilon\} = 1 \] 则称随机变量序列 \(\{X_n\}\) 依概率收敛于 \(a\), 并记作 \(X_n \stackrel{P}{\longrightarrow} a\).
这里可以借鉴高数中极限的定义来类比理解
依概率收敛的性质:
若 \(X_n \stackrel{P}{\longrightarrow} a\), 且 \(g(x)\) 在点 \(a\) 连续, 则 \(g(X_n) \stackrel{P}{\longrightarrow} g(a)\).
若 \(X_n \stackrel{P}{\longrightarrow} a\), \(Y_n \stackrel{P}{\longrightarrow} b\), 且 \(g(x, y)\) 在点 \((a, b)\) 连续, 则 \(g(X_n, Y_n) \stackrel{P}{\longrightarrow} g(a, b)\).
eg:假设 \(X_n \stackrel{P}{\longrightarrow} a,就有X_n^2 \stackrel{P}{\longrightarrow} a^2\)
假设 \(X_n \stackrel{P}{\longrightarrow} a\), \(Y_n \stackrel{P}{\longrightarrow} b\),就有 \(\frac{X_n + Y_n}{2} \stackrel{P}{\longrightarrow} \frac{a + b}{2}\)
切比雪夫大数定律:
设 \(X_1, X_2, ..., X_n, ...\) 是一列两两不相关的随机变量序列, 期望方差均存在, 且方差 \(DX_i\) 一致有界, 即 \(DX_i \le c, i = 1, 2, ...\) 则对 \(\forall \varepsilon > 0\), 有
\[ \lim_{n \to \infty} P\{|\frac{1}{n}\sum_{i=1}^{n}X_i - \frac{1}{n}\sum_{i=1}^{n}EX_i| < \varepsilon\} = 1 \]
特别地, 若 \(X_1, X_2, ..., X_n, ...\) 有相同的期望 \(EX_i = \mu\), 则有
\[ \lim_{n \to \infty} P\{|\frac{1}{n}\sum_{i=1}^{n}X_i - \mu| < \varepsilon\} = 1 \]
辛钦大数定律: 设 \(\{X_n\}\) 为一独立同分布的随机变量序列, 且数学期望存在, \(E(X_i) = \mu\), 则对任意的 \(\varepsilon > 0\), 都有
\[ \lim_{n \to \infty} P\{|\frac{1}{n}\sum_{i=1}^{n}X_i - \mu| < \varepsilon\} = 1 \]
伯努利大数定律: 设 \(f_A\) 是 \(n\) 重伯努利试验中事件 \(A\) 发生的次数, \(p\) 是 \(A\) 在每次试验中发生的概率, 则对任意的 \(\varepsilon > 0\), 都有:
\[\lim_{n \to \infty} P\{|\frac{f_A}{n} - p| < \varepsilon\} = 1 \]
伯努利大数定律说的是当试验次数足够多时,\(频率 \stackrel{P}\longrightarrow 概率\)
下面概括一下切比雪夫大数定律和辛钦大数定律
切比雪夫大数定律:相互独立序列只要方差一致有界,其算术平均值即依概率收敛于期望的算术平均值
辛钦大数定律:独立同分布序列只要期望存在,其算术平均值即依概率收敛于期望
| 特性 | 切比雪夫大数定律 | 辛钦大数定律 |
|---|---|---|
| 分布要求 | 相互独立(可不同分布) | 独立同分布 (i.i.d.) |
| 期望要求 | 必须存在 | 必须存在 |
| 方差要求 | 必须存在且一致有界 | 不要求存在 |
如果题目提到 “独立同分布” 且 “方差未知/可能不存在” → 找辛钦 如果题目提到 “分布不同” 但 “方差有界” → 找切比雪夫。
例题:设随机变量 \(X_1, X_2, ..., X_n\) 相互独立,且均服从于参数为 2 的指数分布, 则当 \(n \to \infty\) 时, \(Y_n = \frac{1}{n}\sum_{i=1}^{n}X_i^2\) 依概率收敛于 ____.
随机变量 \(X_1, X_2, ..., X_n\) 相互独立同分布于参数为 \(2\) 的指数分布,那么\(X_1^2, X_2^2, ..., X_n^2\) 同样相互独立同分布,可以用辛钦大数定律,求一下 \(X^2的期望\)
\(EX^2 = (EX)^2 + DX = (\frac{1}{2})^2 + \frac{1}{4} = \frac{1}{2}\), 所以 \(Y_n = \frac{1}{n}\sum_{i=1}^{n}X_i^2\) 依概率收敛于 \(\frac{1}{2}\)
例题:设 \(X_1, X_2, ..., X_n\) 为独立同分布的随机变量序列, 且概率密度
\[ f(x) = \begin{cases} xe^{-\frac{x^2}{2}}, & x \ge 0, (i=1, 2, ...) \\ 0, & x < 0 \end{cases} \]
问是否存在实数 \(a\), 使得对任意 \(\varepsilon > 0\), 都有 \(\lim_{n \to \infty} P\{|\frac{1}{n}\sum_{i=1}^{n}X_i^2 - a| < \varepsilon\} = 1\)? 若存在, 求 \(a\) 的值; 若不存在, 请说明理由.
已知随机变量 \(X_1, X_2, \dots, X_n\) 相互独立同分布, 由此可知 \(X_1^2, X_2^2, \dots, X_n^2\) 也相互独立同分布.
首先计算 \(X^2\) 的期望 \(EX^2\): \[ \begin{aligned} EX^2 &= \int_{0}^{+\infty} x^2 \cdot xe^{-\frac{x^2}{2}} dx \\ &= \int_{0}^{+\infty} x^3 e^{-\frac{x^2}{2}} dx \\ &= 2 \end{aligned} \]
根据辛钦大数定律,样本均值依概率收敛于总体期望。 对于随机变量序列 \(X_i^2\),其算术平均值应收敛于 \(EX^2 = 2\).
即对任意 \(\varepsilon > 0\),都有: \[\lim_{n \to \infty} P\left\{ \left| \frac{1}{n}\sum_{i=1}^{n}X_i^2 - 2 \right| < \varepsilon \right\} = 1\]
由此得出: \[a = 2\]
5-2. 中心极限定理
列维-林德伯格定理: 设 \(X_1, X_2, ..., X_n, ...\) 是一列独立同分布的随机变量, 且 \(EX_k = \mu, DX_k = \sigma^2 > 0, k = 1, 2, ...\) 则对任意 \(x \in R\) 有
\[ \lim_{n \to \infty} P\{\frac{\sum_{k=1}^{n} X_k - n\mu}{\sqrt{n}\sigma} \le x\} = \Phi(x) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{x} e^{-\frac{t^2}{2}} dt \]
注: 可以简化为如下形式记忆
若 \(X_1, X_2, ..., X_n, ...\) 独立且服从同一分布 \(F(\mu, \sigma^2)\), \(EX = \mu, DX = \sigma^2\), 则当 \(n \to \infty\) 时, \(\sum_{i=1}^{n} X_i\) 近似服从于 \(N(n\mu, n\sigma^2)\).
列维-林德伯格定理简单理解就是当无限个独立同分布的随机变量累加时,得到的新的随机变量服从正态分布
棣莫弗-拉普拉斯定理: 在 \(n\) 重伯努利试验中, 事件 \(A\) 在每次试验中出现的概率为 \(p\) (\(0 < p < 1\)), \(X_n\) 为 \(n\) 次试验中事件 \(A\) 发生的次数, 则对任意 \(x \in R\) 有
\[ \lim_{n \to \infty} P\{\frac{X_n - np}{\sqrt{np(1-p)}} \le x\} = \Phi(x) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{x} e^{-\frac{t^2}{2}} dt \]
棣莫弗-拉普拉斯定理简单理解就是当无限个独立同分布于二项分布的随机变量累加时,得到的新的随机变量服从正态分布
例题:某地区运进一批棉花 1500 包,已知这批棉花每包期望重量为 100 公斤,标准差为 5 公斤,现独立重复抽样 100 包,求这批样本平均重量小于 99.5 公斤的概率。(\(\Phi(1) = 0.8413\))
题目给出 \(\Phi(1) = 0.8413\) 且样本“独立同分布”,暗示了本题考查的是中心极限定理.
设每包棉花的重量为 \(X\),已知总体参数: \[EX = 100, \quad DX = 5^2\]
对于独立重复抽样的 \(n=100\) 包棉花,其样本均值 \(\overline{X}\) 的期望与方差为: \[E\overline{X} = 100, \quad D\overline{X} = \frac{5^2}{100} = \frac{25}{100} = \left(\frac{1}{2}\right)^2\]
由列维-林德伯格定理可知,标准化变量: \[Z = \frac{\overline{X} - 100}{1/2} \sim N(0,1)\]
计算概率过程如下: \[ \begin{aligned} P\{\overline{X} < 99.5\} &= P\left\{ \frac{\overline{X} - 100}{1/2} < \frac{99.5 - 100}{1/2} \right\} \\ &= P\{ Z < -1 \} \\ &= \Phi(-1) \\ &= 1 - \Phi(1) \\ &= 1 - 0.8413 = 0.1587 \end{aligned} \]
第六章-数理统计
%%{init: {'flowchart': {'curve': 'stepAfter'}}}%%
graph LR
classDef hidden fill:none,stroke:none,width:0px,height:0px
A1("数理统计的基本概念")
N1[ ]:::hidden
A1 --- N1
N1 --> B1(总体与样本)
N1 --> B2(经验分布函数)
N1 --> B3(统计量与统计值)
N1 --> B4(三大抽样分布)
N2[ ]:::hidden
B3 --- N2
N2 --> C1(常用统计量)
N2 --> C2(统计量数字特征)
N3[ ]:::hidden
C1 --- N3
N3 --> D1(样本均值)
N3 --> D2(样本方差)
N3 --> D3(样本标准差)
N3 --> D4(样本k阶原点矩)
N3 --> D5(样本k阶中心矩)
N4[ ]:::hidden
B4 --- N4
N4 --> C3(卡方分布)
N4 --> C4(t分布)
N4 --> C5(F分布)
N4 --> C6(正态总体抽样分布)
6-1. 总体和样本
总体:研究对象某项数量指标的全体称为总体.构成总体的每个成员称为个体
eg:研究一批机器的寿命,则全部机器的寿命构成问题的总体,每一台机器的寿命是一个个体
样本: 在相同条件下对总体 \(X\) 进行 \(n\) 次简单随机抽样,得到的 \(n\) 个观察结果 \(X_1, X_2, ..., X_n\) 相互独立且同分布于总体 \(X\), 称 \(X_1, X_2, ..., X_n\) 为来自总体 \(X\) 的一个简单随机样本,简称样本,其中 \(n\) 称为样本容量. 抽样得到的一组实数记为 \(x_1, x_2, ..., x_n\), 称为样本观察值,简称样本值.
eg:从该批机器中随机抽 20 台测定其寿命,即得容量为 20 的样本观测值 \(x_1, x_2, ..., x_{20}\). 抽取前无法预知每台样品的寿命,因此样本 \(X_1, X_2, ..., X_{20}\) 是随机变量.
大写是总体,小写是样本,另外,\(x_1, x_2, ..., x_n \stackrel{iid}{\sim} 总体分布\)
总体和样本符号对照表
| 特征 | 总体参数 | 样本统计量 |
|---|---|---|
| 期望 | \(\mu\) | \(\bar{X}\) |
| 方差 | \(\sigma^2\) | \(S^2\) |
| 标准差 | \(\sigma\) | \(S\) |
| 大小(个数) | \(N\) (通常是无限或很大) | \(n\) (样本容量) |
6-2. 经验分布函数
定义: 设 \(X_1, X_2, ..., X_n\) 为总体 \(X\) 的一个样本,其样本值为 \(x_1, x_2, ..., x_n\), 则称函数 \[ F_n(x) = \frac{\{x_1, x_2, ..., x_n \text{ 中小于或等于 } x \text{ 的个数}\}}{n} \quad (-\infty < x < +\infty) \] 为样本值 \(x_1, x_2, ..., x_n\) 的经验分布函数.
若已知样本值 \(x_1, x_2, ..., x_n\) 的频数、频率分布表为
| 指标 \(X\) | \(x_1^*\) | \(x_2^*\) | … | \(x_l^*\) |
|---|---|---|---|---|
| 频数 \(n_i\) | \(n_1\) | \(n_2\) | … | \(n_l\) |
| 频率 \(f_i\) | \(\frac{n_1}{n}\) | \(\frac{n_2}{n}\) | … | \(\frac{n_l}{n}\) |
则经验分布函数
\(F_n(x) = \begin{cases} 0, & x < x_1^* \\ \frac{n_1 + ... + n_i}{n}, & x_i^* \le x < x_{i+1}^*, \quad (i=1, 2, ..., l-1) \\ 1, & x \ge x_l^* \end{cases}\)
写个题目来了解经验分布函数的写法
设总体 \(X\) 的容量为 10 的一组样本值是 1, 2, 4, 3, 4, 2, 3, 4, 4, 2, 试求样本的经验分布函数.
首先观察到样本值的取值只有1234四种取值情况
下面列出表格
| \(x_i\) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(n_i\) | 1 | 3 | 2 | 4 |
| \(f_i\) | \(\frac{1}{10}\) | \(\frac{3}{10}\) | \(\frac{2}{10}\) | \(\frac{4}{10}\) |
由表格可以写出
\[ F_{10}(x) = \begin{cases} 0, & x < 1 \\ \frac{1}{10}, & 1 \le x < 2 \\ \frac{4}{10}, & 2 \le x < 3 \\ \frac{6}{10}, & 3 \le x < 4 \\ 1, & 4 \le x \end{cases} \]
6-3. 样本统计量
定义: 不含任何未知参数的样本函数 \(g(X_1, X_2, ..., X_n)\) 称为统计量. 设 \(x_1, x_2, ..., x_n\) 是对应于样本 \(X_1, X_2, ..., X_n\) 的样本值,则称 \(g(x_1, x_2, ..., x_n)\) 是 \(g(X_1, X_2, ..., X_n)\) 的观测值,称为统计量值.
例题:设总体 \(X \sim N(\mu, \sigma^2)\), 其中 \(\mu\) 已知, \(\sigma^2\) 未知, \(X_1, X_2\) 是取自总体 \(X\) 的样本, 则下列各量为统计量的是 ( )
|
|
|
|
直接选A,因为 \(\sigma\) 是未知的,统计量不能含有未知参数,只有A是含有已知参数 \(\mu\)
常用统计量:
设 \(X_1, X_2, ..., X_n\) 为总体 \(X\) 的一个样本, \(n\) 为样本容量
样本均值 \(\overline{X} = \frac{1}{n} \sum_{i=1}^{n} X_i\)
样本方差 \(S^2 = \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \overline{X})^2 = \frac{1}{n-1} (\sum_{i=1}^{n} X_i^2 - n\overline{X}^2)\)
样本标准差 \(S = \sqrt{S^2} = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (X_i - \overline{X})^2}\)
样本 \(k\) 阶原点矩 \(A_k = \frac{1}{n} \sum_{i=1}^{n} X_i^k, \quad k = 1, 2, ...,\)
样本 \(k\) 阶中心矩 \(B_k = \frac{1}{n} \sum_{i=1}^{n} (X_i - \overline{X})^k, \quad k = 1, 2, ...,\)
为了便于记忆,我们可以把样本的计算方法看成是模仿总体的计算方法,比如 样本方差 \(S^2\) 就是仿照 \(DX = E(X - EX)^2 = \frac{1}{n} \sum_{i=1}^{n} (X_i - \overline{X})^2\) 写出来的,为了准确,样本方差把分母 \(n\) 修正成了 \(n - 1\),原点矩和中心距是期望和方差更一般的概率,比如期望就是1阶原点矩,方差就是2阶中心距
6-4. 统计量的数字特征
已知 \(X_1, X_2, ..., X_n\) 为来自总体 \(X\) 的样本, \(EX = \mu, DX = \sigma^2\),无论 \(X\) 服从何种分布,都有:
\(EX_i = \mu, \quad DX_i = \sigma^2\);
\(E\overline{X} = \mu, \quad D\overline{X} = \frac{\sigma^2}{n}\);
\(ES^2 = \sigma^2\)
例题:设总体 \(X\) 服从参数为 \(\lambda (\lambda > 0)\) 的泊松分布, \(X_1, X_2, ..., X_n\) 为来自该总体的简单随机样本, 则对于统计量 \(T_1 = \frac{1}{n} \sum_{i=1}^{n} X_i, T_2 = \frac{1}{n-1} \sum_{i=1}^{n-1} X_i + \frac{1}{n} X_n\), 有 ( ).
|
|
|
|
\(EX = \lambda, DX = \lambda\)
\(ET_1 = E\overline{X} = \lambda\)
\(DT_1 = D\overline{X} = \frac{\lambda}{n}\)
\(ET_2 = E(\frac{1}{n-1}\sum_{i=1}^{n-1}X_i + \frac{1}{n}X_n)\)
\(= E(\frac{1}{n-1}\sum_{i=1}^{n-1}X_i) + \frac{1}{n}EX_n\)
\(= \lambda + \frac{\lambda}{n}\)
\(DT_2 = D(\frac{1}{n-1}\sum_{i=1}^{n-1}X_i + \frac{1}{n}X_n)\)
\(= D(\frac{1}{n-1}\sum_{i=1}^{n-1}X_i) + D(\frac{1}{n}X_n)\)
\(= \frac{\lambda}{n-1} + \frac{1}{n^2}\lambda > \frac{\lambda}{n} = T_1\)
选D
6-5. 三大抽样分布与上分位点
统计量的分布称为抽样分布,下面介绍来自正态总体的三大常用统计量的分布
- \(\chi^2\) 分布
定义 设 \(X_1, X_2, ..., X_n\) 是来自总体 N(0, 1) 的样本, 则称统计量
\[ \chi^2 = X_1^2 + X_2^2 + ... + X_n^2 \]
服从自由度为 \(n\) 的 \(\chi^2\) 分布, 记为 \(\chi^2 \sim \chi^2(n)\).
性质
可加性: 设 \(\chi_1^2 \sim \chi^2(n_1)\), \(\chi_2^2 \sim \chi^2(n_2)\), 并且 \(\chi_1^2\), \(\chi_2^2\) 独立, 则 \(\chi_1^2 + \chi_2^2 \sim \chi^2(n_1 + n_2)\)
数学期望和方差: 若 \(\chi^2 \sim \chi^2(n)\), 则有 \(E(\chi^2) = n\), \(D(\chi^2) = 2n\)
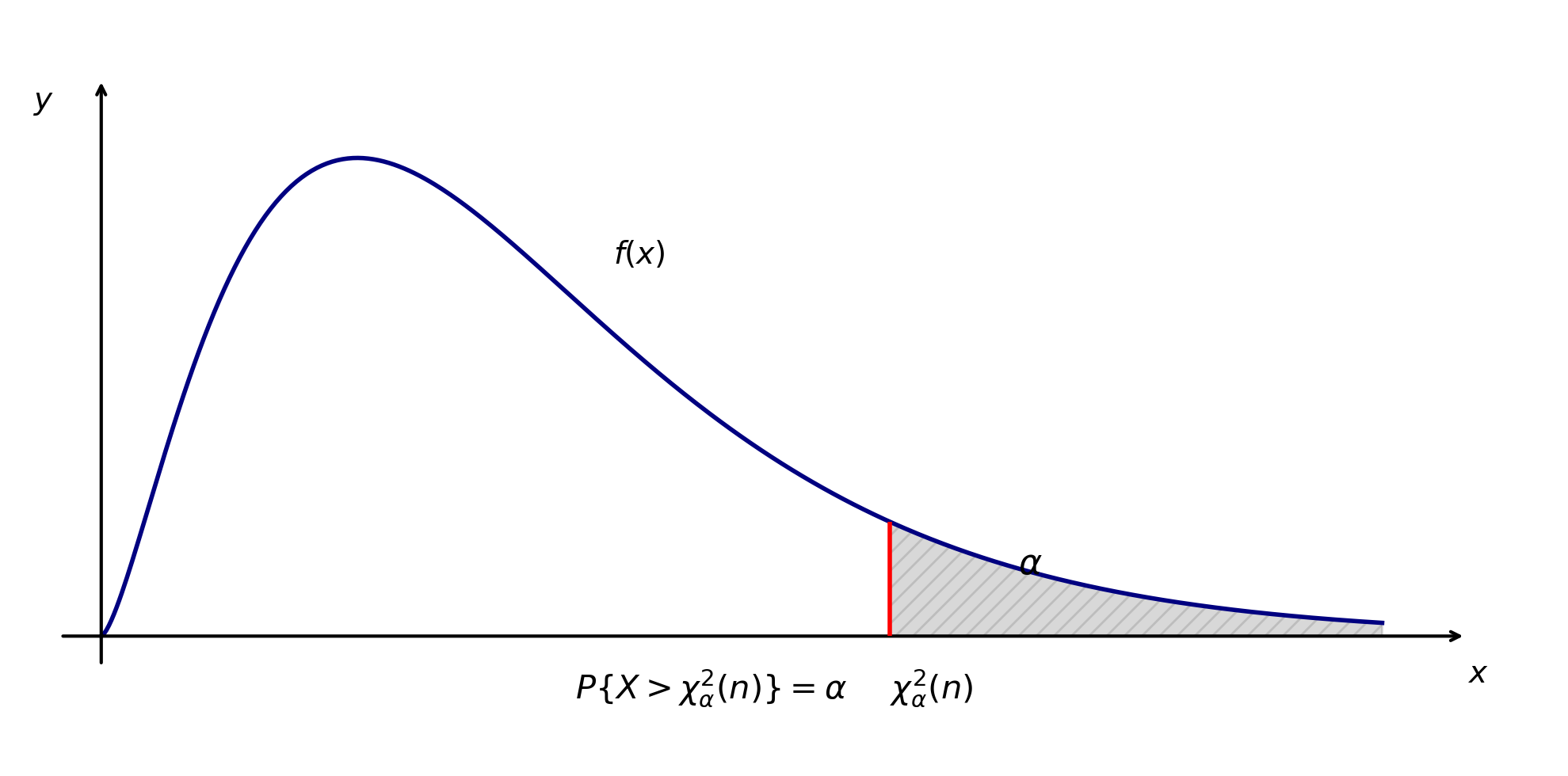
分位点:设有分布函数 \(F(x)\), 对给定的 \(\alpha (0 < \alpha < 1)\), 若有 \(P\{X > x_\alpha\} = \alpha\)
则称点 \(x_\alpha\) 为 \(F(x)\) 的上 \(\alpha\) 分位点.
\(\chi^2(n)\) 的分位点 设 \(\chi^2 \sim \chi^2(n)\), 对给定的 \(\alpha (0 < \alpha < 1)\), 若有 \(\chi_\alpha^2(n) > 0\) 满足
\(P\{\chi^2 > \chi_\alpha^2(n)\} = \alpha\), 则称 \(\chi_\alpha^2(n)\) 为 \(\chi^2(n)\) 分布的上 \(\alpha\) 分位点.
下面作图形象演示一下 \(\chi^2\) 分布的上分位点
- \(t\) 分布
定义 设 \(X \sim N(0, 1)\), \(Y \sim \chi^2(n)\), 且 \(X, Y\) 独立, 则称随机变量
\[ t = \frac{X}{\sqrt{Y/n}} \]
服从自由度为 \(n\) 的 \(t\) 分布, 记为 \(t \sim t(n)\)
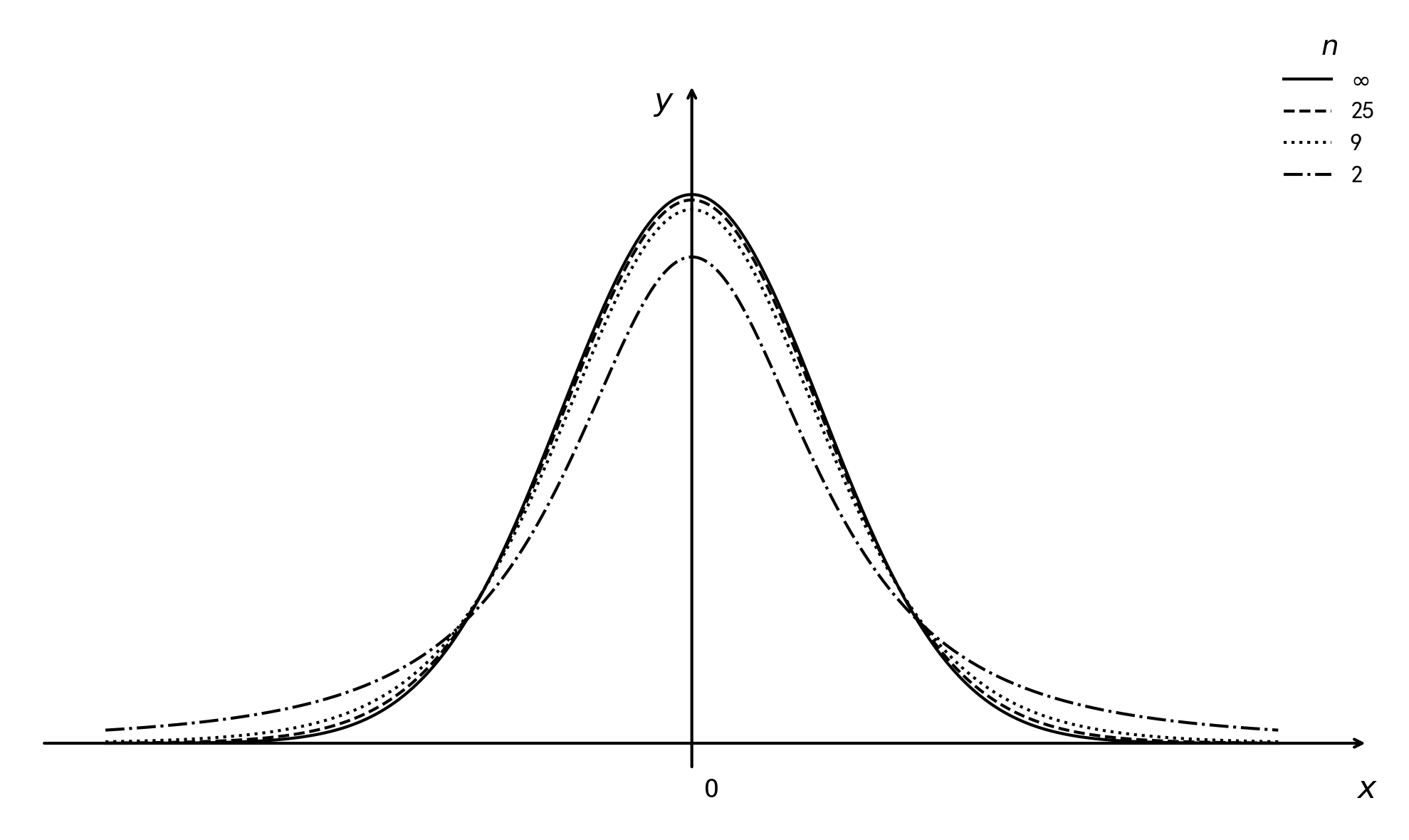
性质
奇偶性: \(t\) 分布的概率密度 \(f(t)\) 图像为偶函数.
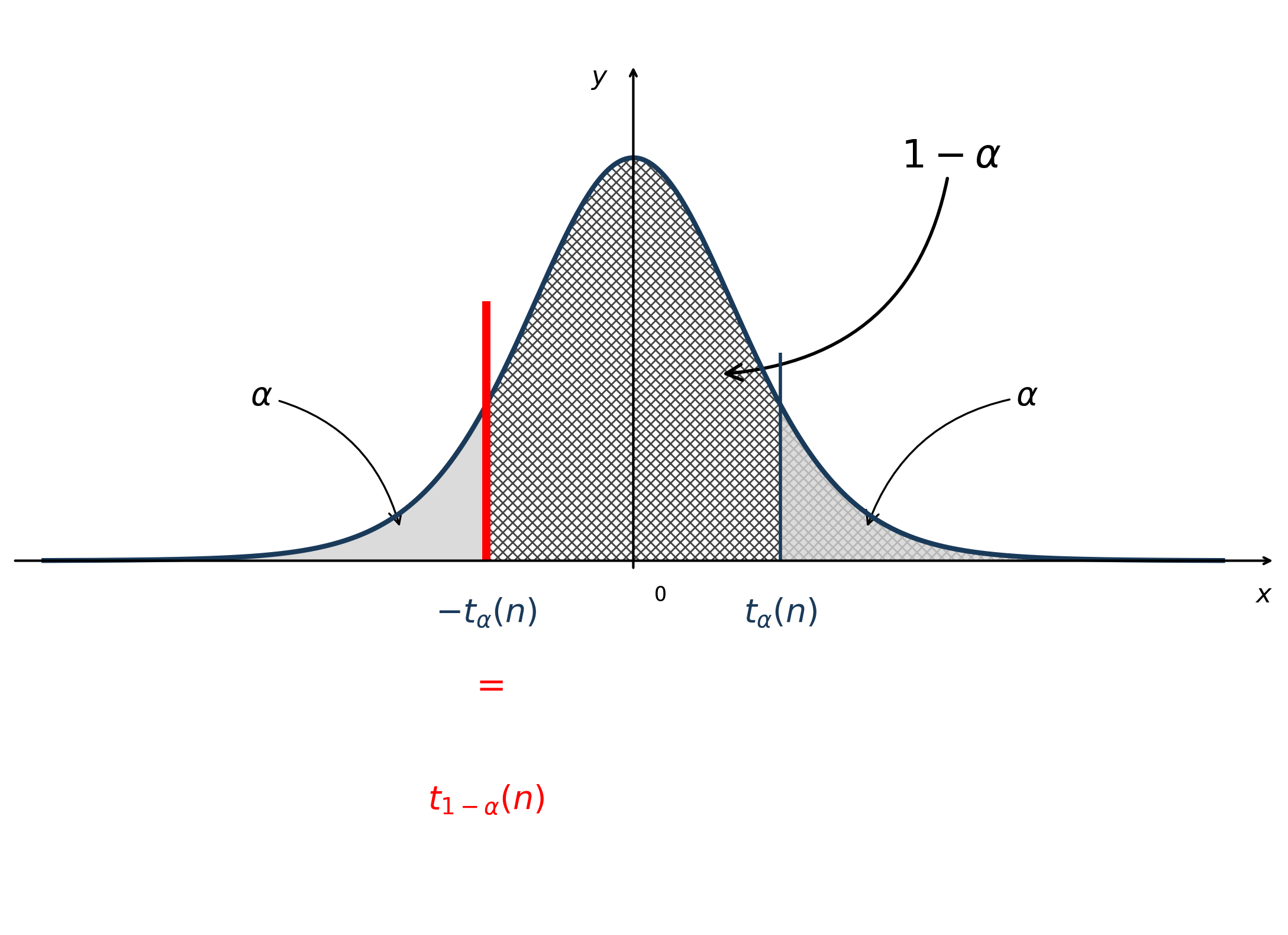
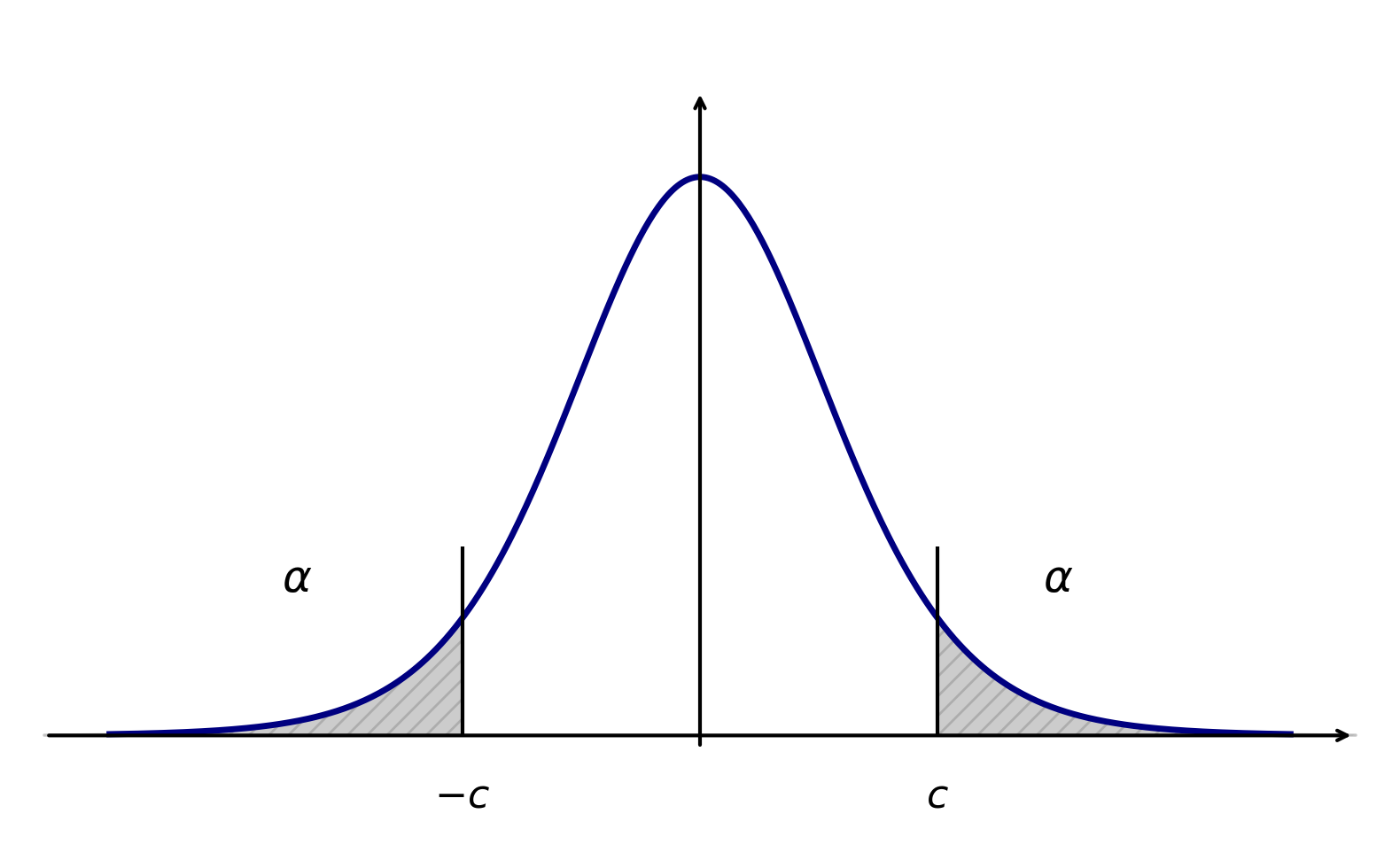
分位点 对于给定的 \(\alpha(0 < \alpha < 1)\), 称满足条件 \(P\{t > t_\alpha(n)\} = \alpha\) 的点 \(t_\alpha(n)\) 为 \(t(n)\) 分布的上 \(\alpha\) 分位点. 易得 \(t_{1-\alpha}(n) = -t_\alpha(n)\).
下面作图直观演示下 \(t\) 分布的上分位点的性质
结论
自由度 \(n = 1\) 的 \(t\) 分布是标准柯西分布,它的期望不存在.
自由度 \(n > 1\) 的 \(t\) 分布期望存在且为 0.
例题:已知 \(X \sim t(n)\) 且 \(P\{X > c\} = \alpha\) 求 \(P\{X^2 > c^2\} = \_\_\_\_.\)
\(P\{X^2 > c^2\}\) = \(P\{X > c\} + P\{X < -c\}\)
\(= 2P\{X > c\}\)
\(= 2\alpha\)
- \(F\) 分布
定义 设 \(X \sim \chi^2(n_1)\), \(Y \sim \chi^2(n_2)\), 且 \(X, Y\) 独立, 则称随机变量
\[ F = \frac{X/n_1}{Y/n_2} \]
服从自由度为 \((n_1, n_2)\) 的 \(F\) 分布, 记为 \(F \sim F(n_1, n_2)\), \(n_1\) 称为第一自由度, \(n_2\) 称为第二自由度.
性质 若 \(F \sim F(n_1, n_2)\), 则 \(\frac{1}{F} \sim F(n_2, n_1)\)
分位点 对于给定的 \(\alpha (0 < \alpha < 1)\), 称满足条件 \(P\{F > F_\alpha(n_1, n_2)\} = \alpha\) 的点 \(F_\alpha(n_1, n_2)\) 为 \(F(n_1, n_2)\) 分布的上 \(\alpha\) 分位点. 易得 \(F_{1-\alpha}(n_1, n_2) = \frac{1}{F_\alpha(n_2, n_1)}\)
这一节主要考小题,出题方式一般是给出一个统计量的表达式,求他服从何种分布,该分布的自由度是多少,下面看3道例题,给出一个结论
\(\chi^2分布\): \(平方和\)
\(t分布\): \(\frac{正态}{\sqrt{平方和}}\)
\(F分布\): \(\frac{平方和}{平方和}\)
例题:设 \(X_1, X_2, ..., X_5\) 为总体 \(X \sim N(0, 1)\) 的一个样本, 设
\(Y = (X_1 + X_2 + X_3)^2 + (X_4 - \sqrt{2}X_5)^2\) 且 \(cY\) 服从 \(\chi^2\) 分布, 则 \(c = \_\_\_\_.\)
一看就是 \(\chi^2分布\),参数是2,至于计算过程,自行去看视频了解,这里不写了 点击跳转到视频讲解链接
例题:设随机变量 \(X, Y\) 相互独立,均服从 \(N(0, 3^2)\) 分布且 \(X_1, X_2, ..., X_9\) 与 \(Y_1, Y_2, ..., Y_9\) 分别是来自总体 \(X, Y\) 的简单随机样本,则统计量 \(U = \frac{X_1 + ... + X_9}{\sqrt{Y_1^2 + ... + Y_9^2}}\) 服从从参数为 ___ 的 ___ 分布.
一看就是 \(t分布\), 参数是9
例题:设总体 \(X\) 服从正态分布 \(X \sim N(0, 2^2)\), 而 \(X_1, X_2, ..., X_{15}\) 是来自总体的简单随机样本, 则随机变量 \(Y = \frac{X_1^2 + ... + X_{10}^2}{2(X_{11}^2 + ... + X_{15}^2)}\) 服从 ___ 分布, 参数为 ___.
一看就是 \(F分布\), 参数是(10,5)
6-6. 正态总体抽样分布
一个正态总体 假设 \(X_1, X_2, ..., X_n\) 是来自正态总体 \(X \sim N(\mu, \sigma^2)\) 的样本, 样本均值与样本方差分别是 \(\overline{X} = \frac{1}{n}\sum_{i=1}^{n}X_i\), \(S^2 = \frac{1}{n-1}\sum_{i=1}^{n}(X_i - \overline{X})^2\), 则
\(\overline{X} \sim N(\mu, \frac{\sigma^2}{n})\), 即 \(\frac{(\overline{X} - \mu)\sqrt{n}}{\sigma} \sim N(0, 1)\);
样本均值 \(\overline{X}\) 与样本方差 \(S^2\) 相互独立;(\(E\overline{X}S^2 = E\overline{X} \cdot ES^2 = \mu \cdot \sigma^2\))
\(\frac{(n-1)S^2}{\sigma^2} = \frac{\sum_{i=1}^{n}(X_i - \overline{X})^2}{\sigma^2} \sim \chi^2(n-1)\); \(\frac{\sum_{i=1}^{n}(X_i - \mu)^2}{\sigma^2} \sim \chi^2(n)\);
\(T = \frac{\overline{X} - \mu}{S/\sqrt{n}} \sim t(n-1)\);
例题:在总体 \(X \sim N(5, 16)\) 中随机地抽取一个容量为 36 的样本 \(X_1, X_2, ..., X_{36}\), 则关于样本均值 \(\overline{X}\) 的概率 \(P\{4 \le \overline{X} \le 6\} = \_\_\_\_.\)
首先确定样本均值 \(\overline{X}\) 的分布: \[\overline{X} \sim N\left(\mu = 5, \frac{\sigma^2}{n} = \frac{16}{36} = \frac{4}{9}\right)\]
接下来对概率不等式进行标准化处理(此时标准差 \(\sigma_{\overline{X}} = \frac{2}{3}\)):
\[ \begin{aligned} P\{4 \le \overline{X} \le 6\} &= P\left\{ \frac{4-5}{2/3} \le \frac{\overline{X}-5}{2/3} \le \frac{6-5}{2/3} \right\} \\ &= P\left\{ -\frac{3}{2} \le Z \le \frac{3}{2} \right\} \\ &= \Phi\left( \frac{3}{2} \right) - \Phi\left( -\frac{3}{2} \right) \\ &= 2\Phi(1.5) - 1 \end{aligned} \]
性质3中第一个,不作证明,第二个 \(\frac{\sum_{i=1}^{n}(X_i - \mu)^2}{\sigma^2} \sim \chi^2(n)\) 证明:
由 \(\frac{X_i - \mu}{\sigma} \stackrel{iid}{\sim} N(0, 1)\) ,那么平方之后,就是n个标准正态分布求和,所以服从 \(\chi^2\) 分布,自由度是 \(n, 由此\rightarrow \sum_{i=1}^{n}(\frac{X_i - \mu}{\sigma})^2 \sim \chi^2(n)\)
性质4证明:\(\frac{\frac{\overline{X} - \mu}{\sigma / \sqrt{n}}}{\sqrt{\frac{(n-1)S^2}{\sigma^2} / (n-1)}} \sim t(n-1)\)
例题:设 \(X_1, X_2, ..., X_n (n \ge 2)\) 为来自总体 \(N(0, 1)\) 的简单随机样本, \(\overline{X}\) 为样本均值, \(S^2\) 为样本方差, 则 ( )
| (A) \(n\overline{X} \sim N(0, 1)\) | (B) \(nS^2 \sim \chi^2(n)\) |
| (C) \(\frac{(n-1)\overline{X}}{S} \sim t(n-1)\) | (D) \(\frac{(n-1)X_1^2}{\sum_{i=2}^{n}X_i^2} \sim F(1, n-1)\) |
选项 A:分析期望与方差 \[ \begin{aligned} E(n\overline{X}) &= nE\overline{X} = n\mu = n \cdot 0 = 0 \\ D(n\overline{X}) &= n^2 D\overline{X} = n^2 \cdot \frac{\sigma^2}{n} = n^2 \cdot \frac{1}{n} = n \\ &\therefore n\overline{X} \sim N(0, n) \end{aligned} \]
选项 B:利用抽样分布定理 直接套用标准公式:\(\frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1)\) 由于题目中 \(\sigma^2 = 1\),应有: \[(n-1)S^2 \sim \chi^2(n-1)\] 此处选项给出的是 \(n\) 而不是 \(n-1\),故错误.
选项 C:构造 t 分布统计量 已知 \(\frac{\overline{X} - \mu}{S/\sqrt{n}} \sim t(n-1)\),代入 \(\mu = 0\): \[\frac{\overline{X} - 0}{S / \sqrt{n}} = \frac{\sqrt{n}\overline{X}}{S} \sim t(n-1)\] 故选项 C 的表达式形式不对.
选项 D:利用 F 分布定义 \[ \begin{aligned} \text{由于 } X_i \sim N(0,1) \Rightarrow &X_1^2 \sim \chi^2(1) \\ &\sum_{i=2}^{n}X_i^2 \sim \chi^2(n-1) \\ \text{由 } F = \frac{U/n_1}{V/n_2} \text{ 得:} &\frac{X_1^2 / 1}{(\sum_{i=2}^{n}X_i^2) / (n-1)} = \frac{(n-1)X_1^2}{\sum_{i=2}^{n}X_i^2} \sim F(1, n-1) \end{aligned} \]
结论:D 正确
第七章-点估计与估计量的评价
%%{init: {'flowchart': {'curve': 'stepAfter'}}}%%
graph LR
classDef hidden fill:none,stroke:none,width:0px,height:0px
A1("点估计与估计量的评价")
N1[ ]:::hidden
A1 --- N1
N1 --> B1(点估计)
N1 --> B2(估计量的评价)
N2[ ]:::hidden
B1 --- N2
N2 --> C1(矩估计)
N2 --> C2(最大似然估计)
N3[ ]:::hidden
C1 --- N3
N3 --> D1(离散型总体)
N3 --> D2(连续型总体)
N4[ ]:::hidden
C2 --- N4
N4 --> D3(似然函数有极值)
N4 --> D4(似然函数单调)
N5[ ]:::hidden
B2 --- N5
N5 --> C3(无偏性)
N5 --> C4(有效性)
N5 --> C5("一致性(相合性)")
7.1 矩估计
矩估计法定义: 用样本矩估计同阶的总体矩,用样本矩的函数估计总体矩的函数,这种估计法称为参数的矩估计。
步骤 估计 \(k\) 个未知参数 \(\theta_1, \theta_2, ..., \theta_k\), \(X_1, X_2, ..., X_n\) 为来自总体 \(X\) 样本, 令
\[ \frac{1}{n}\sum_{i=1}^{n}X_i^l = EX^l \quad (l = 1, 2, ..., k) \]
解得 \(\hat{\theta_l} = \theta(X_1, ..., X_n)\), \(l = 1, 2, ..., k\)
例题:设总体 \(X\) 的概率分布为
| \(X\) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| \(P\) | \(\theta^2\) | \(2\theta(1-\theta)\) | \(\theta^2\) | \(1-2\theta\) |
其中 \(\theta (0 < \theta < \frac{1}{2})\) 是未知参数, 利用总体 \(X\) 的如下样本值 3,1,3,0,3,1,2,3, 求 \(\theta\) 的矩估计值.
像这种只有一个未知量的,直接用 \(\overline{X} = EX\) 一个方程就能解决。
\[ \begin{aligned} EX &= 0 \cdot \theta^2 + 1 \cdot 2\theta(1-\theta) + 2 \cdot \theta^2 + 3 \cdot (1-2\theta) \\ &= 2\theta - 2\theta^2 + 2\theta^2 + 3 - 6\theta \\ &= 3 - 4\theta \end{aligned} \]
令 \(\overline{X} = EX = 3 - 4\theta \Rightarrow \hat{\theta} = \frac{3 - \overline{X}}{4}\)
注意:题目求的是矩估计值,应该是一个具体的数;如果求的是矩估计量,到上一步就结束了。
\[ \begin{aligned} \overline{x} &= \frac{1}{8}(3+1+3+0+3+1+2+3) = 2 \\ &\therefore \text{矩估计值 } \hat{\theta} = \frac{3 - 2}{4} = \frac{1}{4} \end{aligned} \]
例题:设总体 \(X \sim N(\mu, \sigma^2)\), 其中 \(\mu, \sigma^2\) 是未知参数, \(X_1, X_2, ..., X_n\) 是取自总体 \(X\) 的一个简单随机样本, 求 \(\mu, \sigma^2\) 的矩估计量.
像这种只有两个未知量的,用 \(\overline{X} = EX,\frac{1}{n}\sum_{i=1}^{n}(X_i - \overline{X})^2 = DX\) 两个方程就能解决
\[ \begin{cases} \overline{X} = EX = \mu \\ \frac{1}{n}\sum_{i=1}^{n}(X_i - \overline{X})^2 = DX = \sigma^2 \end{cases} \Rightarrow \begin{cases} \hat{\mu} = \overline{X} \\ \hat{\sigma^2} = \frac{1}{n}\sum_{i=1}^{n}(X_i - \overline{X})^2 \end{cases} \]
7.2 最大似然估计
似然估计:
离散型总体 \(X\) 设 \(P\{X = a_i\} = p(a_i; \theta), i = 1, 2, ..., \theta \in \Theta\), 则称
\(L(\theta) = L(x_1, ..., x_n; \theta) = \prod_{i=1}^{n} p(x_i; \theta)\)
为该总体的似然函数.
连续型总体 \(X\) 设 \(X \sim f(x; \theta), \theta \in \Theta\), 则称
\(L(\theta) = L(x_1, ..., x_n; \theta) = \prod_{i=1}^{n} f(x_i; \theta)\)
为该总体的似然函数.
注: 将似然函数 \(L(\theta)\) 理解为 “恰好取到样本值 \(x_1, ..., x_n\)” 的概率.
最大似然估计:
固定样本值 \(x_1, x_2, ..., x_n\), 在 \(\theta \in \Theta\) 内使似然函数 \(L(\theta) = L(x_1, ..., x_n; \theta)\) 达到最大的参数值 \(\theta(x_1, ..., x_n)\), 作为参数 \(\theta\) 的估计值.
求最大似然估计的步骤 (以连续型总体 \(X \sim f(x; \theta)\) 为例)
构造似然函数 \(L(\theta) = L(x_1, ..., x_n; \theta) = \prod_{i=1}^{n} f(x_i; \theta)\);
取对数 \(\ln L(\theta) = L(x_1, ..., x_n; \theta) = \sum_{i=1}^{n} \ln f(x_i; \theta)\);
一个参数 解似然方程 \(\frac{d[\ln L(\theta)]}{d\theta} = 0\), 若有解,即为最大似然估计 \(\hat{\theta}\).
两个参数 解似然方程 \(\begin{cases} \frac{\partial \ln L(\theta_1, \theta_2)}{\partial \theta_1} = 0 \\ \frac{\partial \ln L(\theta_1, \theta_2)}{\partial \theta_2} = 0 \end{cases}\), 若有解,即为最大似然估计 \(\hat{\theta_1}, \hat{\theta_2}\).
例题:设总体 \(X\) 的概率分布为
| \(X\) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| \(P\) | \(\theta^2\) | \(2\theta(1-\theta)\) | \(\theta^2\) | \(1-2\theta\) |
其中 \(\theta (0 < \theta < \frac{1}{2})\) 是未知参数, 利用总体 \(X\) 的如下样本值 3,1,3,0,3,1,2,3, 求 \(\theta\) 的最大似然估计值.
样本值中0一共出现了1次,发生的概率是 \(\theta^2\)
样本值中1一共出现了2次,发生的概率是 \((2\theta(1-\theta))^2\)
样本值中2一共出现了1次,发生的概率是 \(\theta^2\)
样本值中3一共出现了4次,发生的概率是 \((1-2\theta)^4\)
\(L(\theta) = \theta^2 \cdot [2\theta(1-\theta)]^2 \cdot \theta^2 \cdot (1-2\theta)^4 = 4\theta^6(1-\theta)^2(1-2\theta)^4\)
取 \(\ln L(\theta) = \ln 4 + 6\ln \theta + 2\ln (1-\theta) + 4\ln (1-2\theta)\)
令 \(\frac{d\ln L(\theta)}{d\theta} = \frac{6}{\theta} - \frac{2}{1-\theta} - \frac{8}{1-2\theta} = 0\)
解得 \(\theta = \frac{7 + \sqrt{13}}{12}\) 或 \(\frac{7 - \sqrt{13}}{12}\) (因为 \(\theta > \frac{1}{2}\) 舍去)
例题:设某种元件的使用寿命 \(X\) 的概率密度为
\(f(x;\theta) = \begin{cases} 2e^{-2(x-\theta)}, & x > \theta \\ 0, & x \le \theta \end{cases}\)
其中 \(\theta > 0\) 为未知参数. 设 \(x_1, x_2, ..., x_n\) 是 \(X\) 的一组样本观测值, 求 \(\theta\) 的最大似然估计量.
当 \(x_1, ..., x_n > \theta\) 时,似然函数为:
\[ \begin{aligned} L(\theta) &= \prod_{i=1}^{n} f(x_i; \theta) = 2^n e^{-2\sum_{i=1}^{n}x_i + 2n\theta} \\ \ln L(\theta) &= n\ln 2 - 2\sum_{i=1}^{n}x_i + 2n\theta \\ \frac{d\ln L(\theta)}{d\theta} &= 2n > 0 \end{aligned} \]
所以 \(L(\theta)\) 是一个单增的函数.
由于 \(f(x;\theta)\) 中,任意的 \(x_i > \theta\), 意味着 \(\theta < \min\{x_1, x_2, ..., x_n\}\),
要使 \(L(\theta)\) 最大,\(\theta\) 应取其能达到的最大值 \(\min\{x_1, x_2, ..., x_n\}\).
因此,\(\theta\) 的最大似然估计量为: \[\hat{\theta} = \min\{X_1, X_2, ..., X_n\}\]
例题:设 \(x_1, x_2, ..., x_n\) 是来自总体 \(X \sim N(\mu, \sigma^2)\) ( \(\mu, \sigma^2\) 均未知) 的简单随机样本的观测值, 求 \(\mu\) 和 \(\sigma^2\) 的最大似然估计值.
\(f(x; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}, -\infty < x < +\infty\)
\(L(\mu, \sigma^2) = \prod_{i=1}^{n} f(x_i; \mu, \sigma^2)\)
\(= \frac{1}{(2\pi)^{\frac{n}{2}}\sigma^n} e^{-\frac{1}{2\sigma^2}\sum_{i=1}^{n}(x_i - \mu)^2}\)
\(\ln L(\mu, \sigma^2) = -\frac{n}{2}\ln 2\pi - \frac{n}{2}\ln \sigma^2 - \frac{1}{2\sigma^2}\sum_{i=1}^{n}(x_i - \mu)^2\)
\(\begin{cases} \frac{\partial \ln L(\mu, \sigma^2)}{\partial \mu} = \frac{1}{\sigma^2}\sum_{i=1}^{n}(x_i - \mu) = 0 \\\\ \frac{\partial \ln L(\mu, \sigma^2)}{\partial \sigma^2} = -\frac{n}{2} \cdot \frac{1}{\sigma^2} + \frac{1}{2(\sigma^2)^2}\sum_{i=1}^{n}(x_i - \mu)^2 = 0 \end{cases} \Rightarrow \begin{cases} \hat{\mu} = \frac{1}{n}\sum_{i=1}^{n}x_i = \overline{X} \\ \hat{\sigma^2} = \frac{1}{n}\sum_{i=1}^{n}(x_i - \mu)^2 = \frac{1}{n}\sum_{i=1}^{n}(x_i - \overline{X})^2 \end{cases}\)
7.3 估计量的评价标准
无偏性: 设 \(\hat{\theta} = \theta(X_1, X_2, ..., X_n)\) 是未知参数 \(\theta\) 的估计量, 若 \(E(\hat{\theta})\) 存在, 且对 \(\forall \theta \in \Theta\) 有 \(E(\hat{\theta}) = \theta\), 则称 \(\hat{\theta}\) 是 \(\theta\) 的无偏估计量, 称 \(\hat{\theta}\) 具有无偏性.
有效性: 设 \(\hat{\theta_1} = \theta_1(X_1, X_2, ..., X_n)\) 与 \(\hat{\theta_2} = \theta_2(X_1, X_2, ..., X_n)\) 都是 \(\theta\) 的无偏估计量, 若有 \(D(\hat{\theta_1}) < D(\hat{\theta_2})\), 则称 \(\hat{\theta_1}\) 比 \(\hat{\theta_2}\) 更有效.
一致性: 设 \(\hat{\theta}\) 是 \(\theta\) 的估计量, 若对 \(\forall \theta \in \Theta\), 有 \(\lim_{n \to \infty} P\{|\hat{\theta} - \theta| < \varepsilon\} = 1\), 即 \(\hat{\theta} \xrightarrow{P} \theta\), 则称 \(\hat{\theta}\) 是 \(\theta\) 的一致估计量.
例题:设总体 \(X\) 的概率密度为
\[ f(x; \theta) = \begin{cases} \frac{6x}{\theta^3}(\theta - x), & 0 < x < \theta, \\ 0, & 其他, \end{cases} \]
设 \(X_1, X_2, ..., X_n\) 是来自 \(X\) 的一个简单随机样本, 求未知参数 \(\theta\) 的矩估计量 \(\hat{\theta}\), 并判断 \(\hat{\theta}\) 是否为 \(\theta\) 的无偏估计.
\(EX = \int_{-\infty}^{+\infty} x f(x; \theta) dx\)
\(= \int_{0}^{\theta} x \cdot \frac{6x}{\theta^3}(\theta - x) dx = \frac{\theta}{2}\)
令 \(\overline{X} = EX = \frac{\theta}{2} \Rightarrow \hat{\theta} = 2\overline{X}\). 其中 \(\overline{X} = \frac{1}{n}\sum_{i=1}^{n}x_i\)
\(E\hat{\theta} = E(2\overline{X}) = 2E\overline{X} = 2EX = 2 \cdot \frac{\theta}{2} = \theta\)
\(\therefore \hat{\theta}\) 是 \(\theta\) 的无偏估计.
例题:取容量 \(n = 3\) 的样本 \(X_1, X_2, X_3\), 证明总体均值 \(\mu\) 的三个无偏估计量
\(\hat{\mu_1} = \overline{X} = \frac{1}{3}\sum_{i=1}^{3}X_i\), \(\hat{\mu_2} = \frac{1}{2}X_1 + \frac{1}{3}X_2 + \frac{1}{6}X_3\), \(\hat{\mu_3} = X_1\) 中, \(\hat{\mu_1} = \overline{X}\) 比 \(\hat{\mu_2}, \hat{\mu_3}\) 都有效.
设总体方差为 \(\sigma^2\)
\[ \begin{aligned} D\hat{\mu}_1 &= D\overline{X} = \frac{\sigma^2}{3} \\ D\hat{\mu}_2 &= D\left(\frac{1}{2}X_1 + \frac{1}{3}X_2 + \frac{1}{6}X_3\right) \\ &= \frac{1}{4}DX_1 + \frac{1}{9}DX_2 + \frac{1}{36}DX_3 \\ &= \frac{7}{18}\sigma^2 \\ D\hat{\mu}_3 &= DX_1 = \sigma^2 \end{aligned} \]
有 \(D\hat{\mu}_1 < D\hat{\mu}_2 < D\hat{\mu}_3\)
\(\therefore \hat{\mu}_1\) 最有效.
第八章-区间估计
%%{init: {'flowchart': {'curve': 'stepAfter'}}}%%
graph LR
classDef hidden fill:none,stroke:none,width:0px,height:0px
A1("区间估计")
N1[ ]:::hidden
A1 --- N1
N1 --> B1(概念与原理)
N1 --> B2(置信区间)
N1 --> B3(置信水平)
N2[ ]:::hidden
B2 --- N2
N2 --> C1(单个正态总体)
N3[ ]:::hidden
C1 --- N3
N3 --> D1(均值)
N3 --> D2(方差)
8.1 概念、原理与公式
区间估计定义:设总体 \(X\) 的分布中含有一个未知参数 \(\theta\). 若对于给定的概率 \(1-\alpha(0 < \alpha < 1)\), 存在两个统计量 \(\hat{\theta_1} = \hat{\theta_1}(X_1, X_2, ..., X_n)\) 与 \(\hat{\theta_2} = \hat{\theta_2}(X_1, X_2, ..., X_n)\), 使得
\[ P\{\hat{\theta_1} \le \theta \le \hat{\theta_2}\} = 1 - \alpha \]
则随机区间 \((\hat{\theta_1}, \hat{\theta_2})\) 称为参数 \(\theta\) 的置信水平(或置信度)为 \(1-\alpha\) 的置信区间(或区间估计), \(\hat{\theta_1}\) 称为置信下限, \(\hat{\theta_2}\) 称为置信上限, \(1-\alpha\) 称为置信水平.
之前的正态总体抽样分布再来回顾一下:
\(\overline{X} \sim N(\mu, \frac{\sigma^2}{n})\), 即 \(\frac{(\overline{X} - \mu)\sqrt{n}}{\sigma} \sim N(0, 1)\);
样本均值 \(\overline{X}\) 与样本方差 \(S^2\) 相互独立;(\(E\overline{X}S^2 = E\overline{X} \cdot ES^2 = \mu \cdot \sigma^2\))
\(\frac{(n-1)S^2}{\sigma^2} = \frac{\sum_{i=1}^{n}(X_i - \overline{X})^2}{\sigma^2} \sim \chi^2(n-1)\); \(\frac{\sum_{i=1}^{n}(X_i - \mu)^2}{\sigma^2} \sim \chi^2(n)\);
\(T = \frac{\overline{X} - \mu}{S/\sqrt{n}} \sim t(n-1)\);
正态总体参数的双侧区间估计表:
| 待估参数 | 条件 | 统计量 | 双侧置信区间 |
|---|---|---|---|
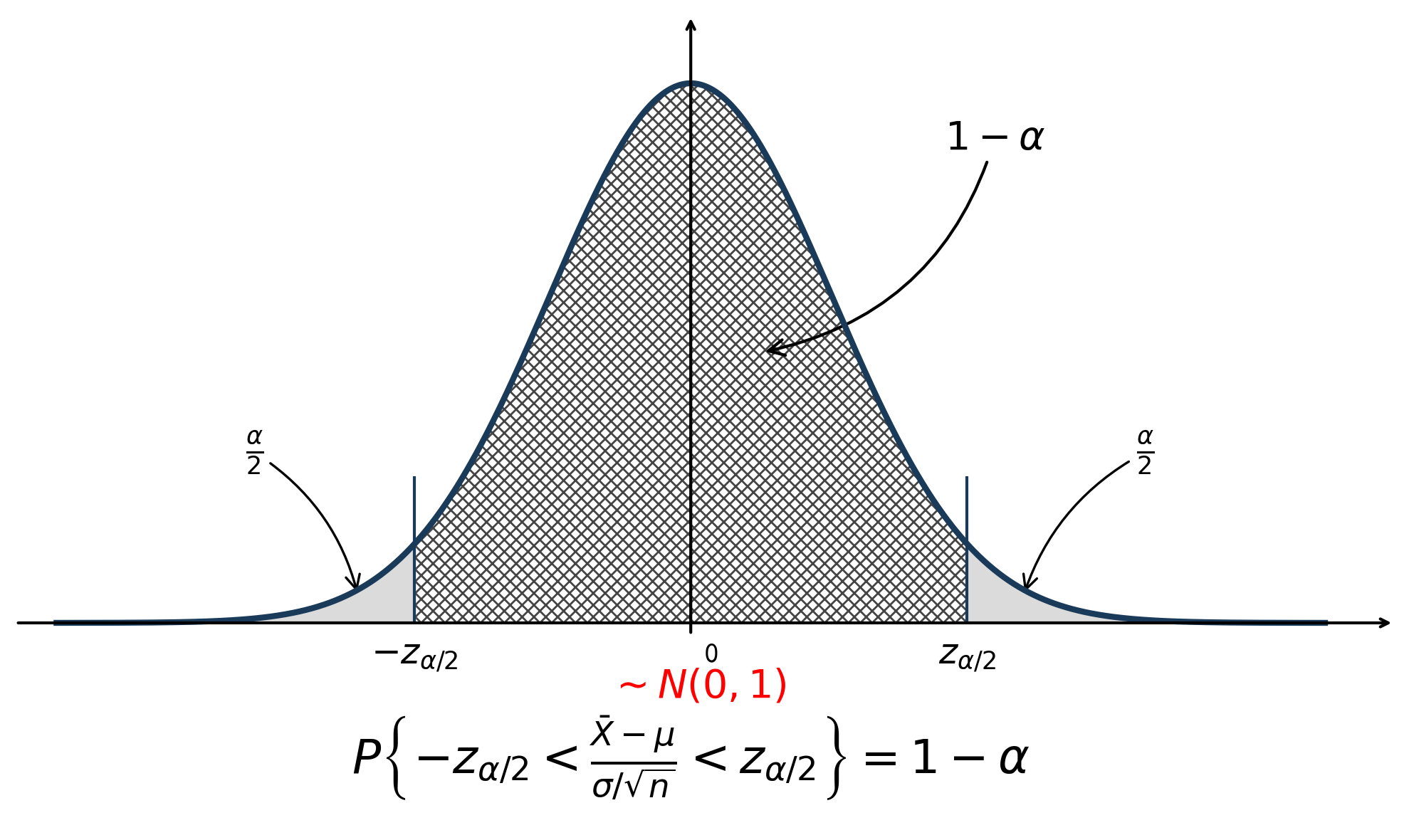
| 均值 \(\mu\) | \(\sigma^2\) 已知 | \(\frac{\bar{X}-\mu}{\sigma/\sqrt{n}} \sim N(0,1)\) | \(\left[ \bar{X}-z_{\alpha/2} \frac{\sigma}{\sqrt{n}}, \bar{X}+z_{\alpha/2} \frac{\sigma}{\sqrt{n}} \right]\) |
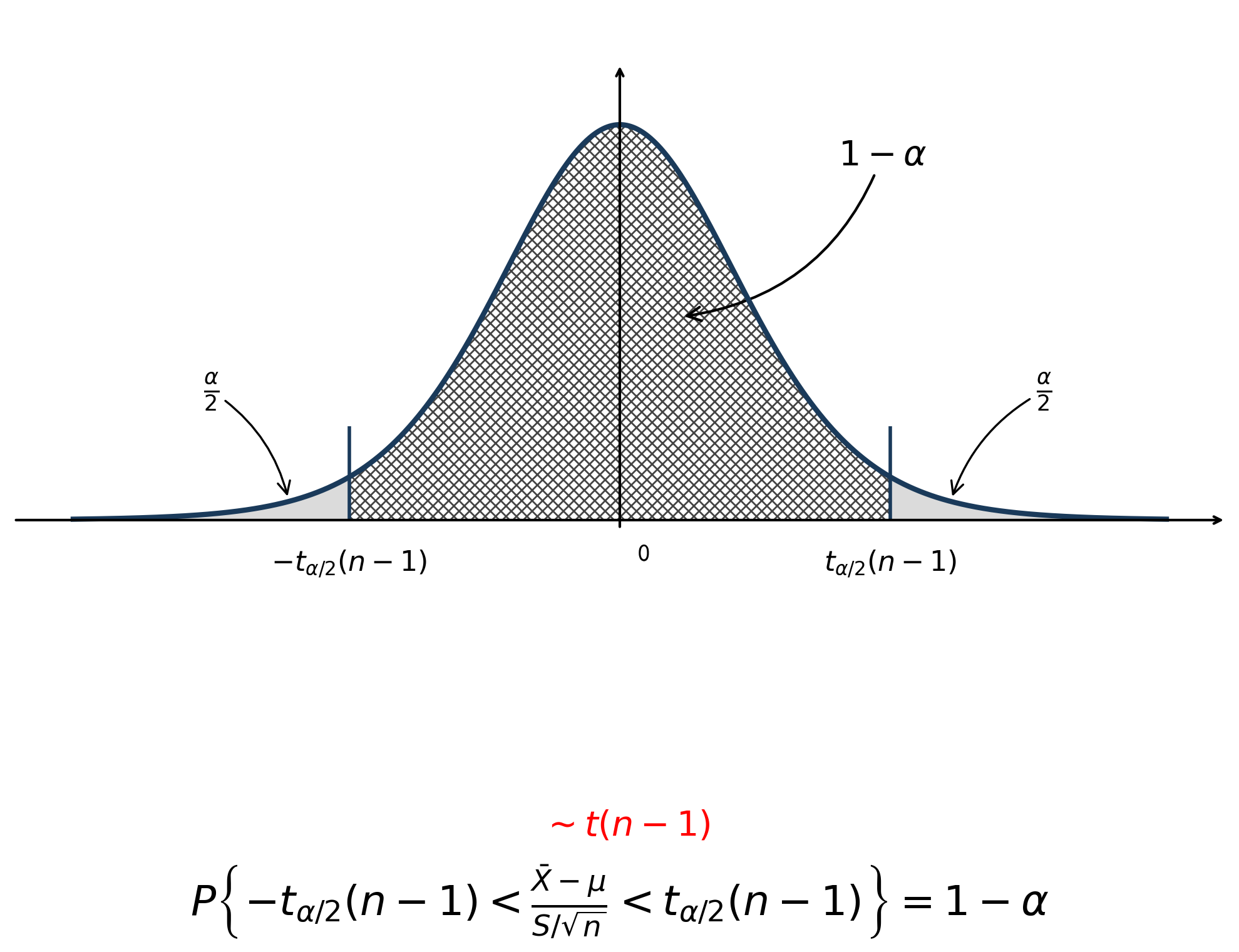
| \(\sigma^2\) 未知 | \(\frac{\bar{X}-\mu}{S/\sqrt{n}} \sim t(n-1)\) | \(\left[ \bar{X}-t_{\alpha/2}(n-1) \frac{S}{\sqrt{n}}, \bar{X}+t_{\alpha/2}(n-1) \frac{S}{\sqrt{n}} \right]\) | |
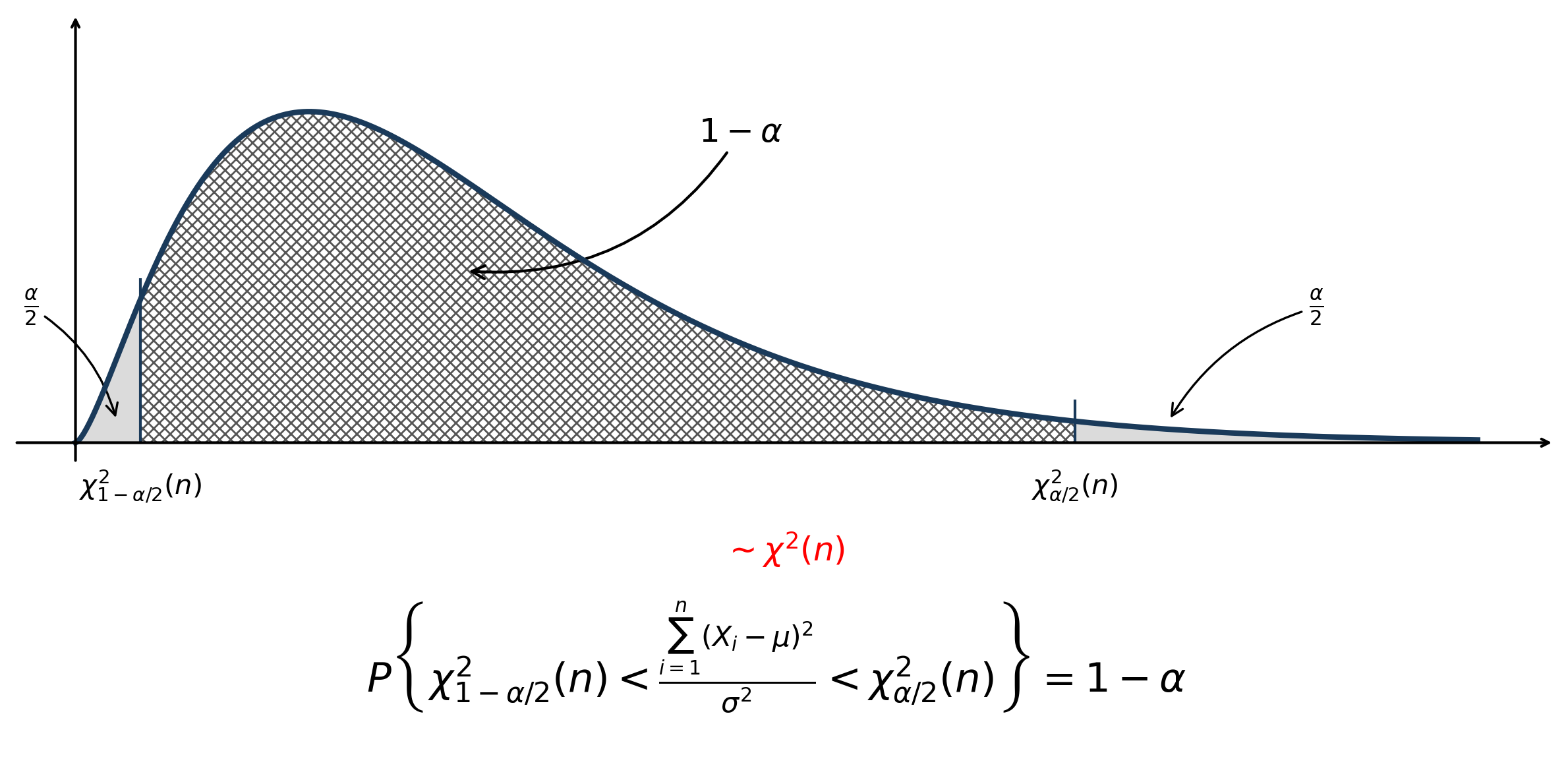
| 方差 \(\sigma^2\) | \(\mu\) 已知 | \(\frac{\sum_{i=1}^{n}(X_i-\mu)^2}{\sigma^2} \sim \chi^2(n)\) | \(\left[ \frac{\sum (X_i-\mu)^2}{\chi_{\alpha/2}^2(n)}, \frac{\sum (X_i-\mu)^2}{\chi_{1-\alpha/2}^2(n)} \right]\) |
| \(\mu\) 未知 | \(\frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1)\) | \(\left[ \frac{(n-1)S^2}{\chi_{\alpha/2}^2(n-1)}, \frac{(n-1)S^2}{\chi_{1-\alpha/2}^2(n-1)} \right]\) |
下面逐一推导:
- 待估参数:\(\mu\)
- \(\sigma^2已知\)
- \(\sigma^2未知\)
- 待估参数:\(\sigma^2\)
- \(\mu 已知\)
- \(\mu 未知\)
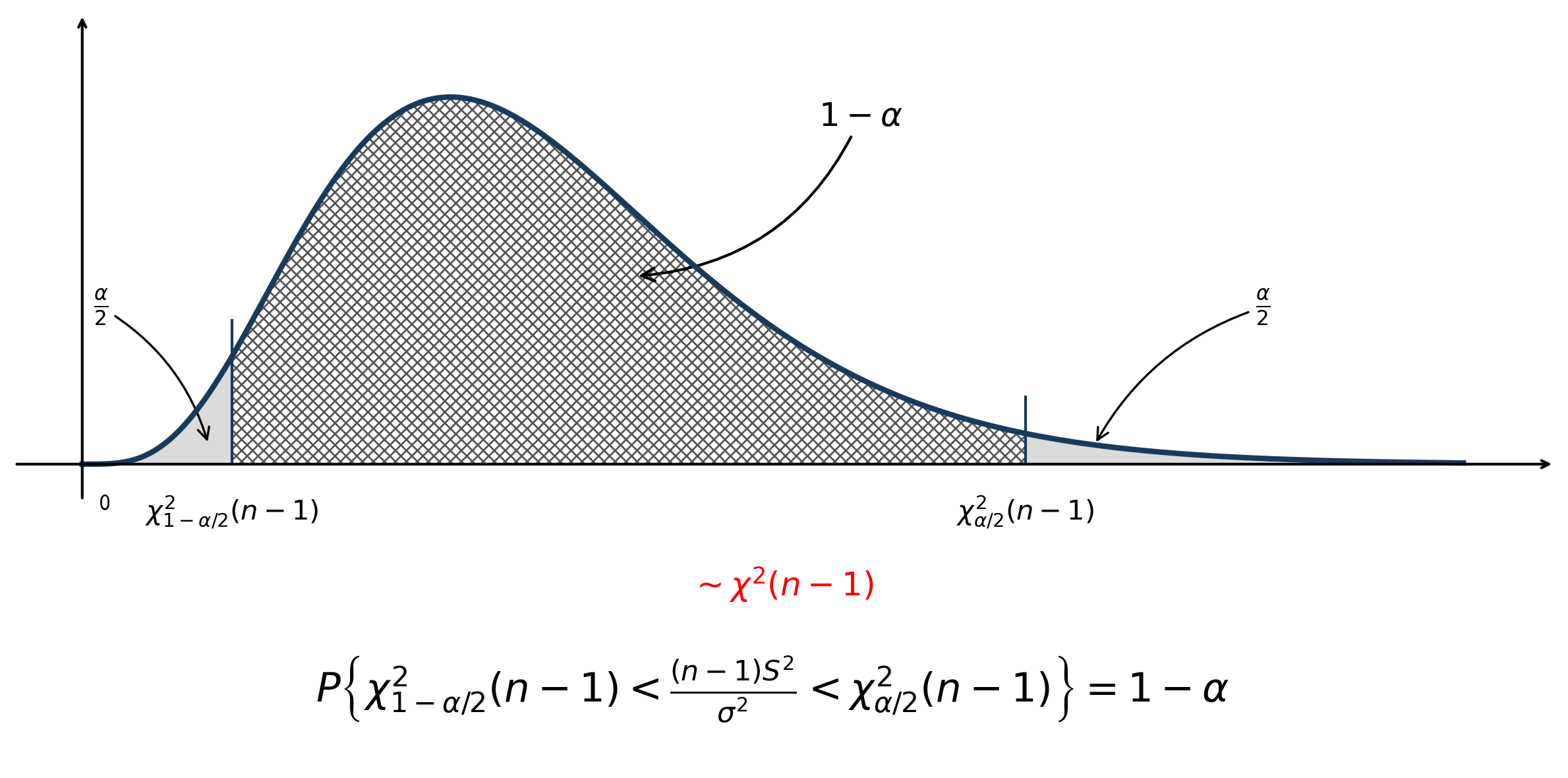
8.2 单个正态总体的均值和方差的置信区间
例题:设一批零件的长度服从正态分布 \(N(\mu, \sigma^2)\), 其中 \(\mu, \sigma^2\) 均未知. 现从中随机抽取 16 个零件, 测得样本均值 \(\overline{x} = 20 (cm)\), 样本标准差 \(s = 1 (cm)\), 则 \(\mu\) 的置信度为 0.90 的置信区间是 ( )
|
|
|
|
这个题在 \(\sigma^2 未知的情况下,求 \mu 的置信区间,1- \alpha = 0.90, \alpha = 0.10,套公式选D\)
例题:设冷钢丝的折断力服从正态分布, 从一批铜丝中任取 10 根, 测试折断力, 得数据为 578, 572, 570, 568, 572, 570, 570, 596, 584, 572. 求: (1) 样本均值和样本方差; (2) 方差的置信区间 (\(\alpha = 0.05\)).
(1).
\[ \overline{x} = \frac{1}{10}\sum_{i=1}^{10}x_i = 575.2 \] \[ S^2 = \frac{1}{9}\sum_{i=1}^{10}(x_i - \overline{x})^2 = 75.73 \]
(2).
\(\mu\) 未知,求 \(\sigma^2\) 的置信区间:
\((\frac{(n-1)S^2}{\chi_{\alpha/2}^2(n-1)}, \frac{(n-1)S^2}{\chi_{1-\alpha/2}^2(n-1)})\)
\(= (\frac{9 \times 75.73}{19.0228}, \frac{9 \times 75.73}{2.7004})\)
\(= (35.83, 252.40)\)
