概率论期末备考

概率论期末备考

以下内容均来自 【【Kira老师】《概率论与数理统计》大学生零基础精讲课25h（已完结）| 26考研基础阶段适用】 我只会列出我觉得重要的点 alt text

第一章-随机事件和概率

%%{init: {'flowchart': {'curve': 'stepAfter'}}}%%
graph LR
    %% 定义隐藏节点样式
    classDef hidden fill:none,stroke:none,width:0px,height:0px
    
    A1(随机事件和概率)
    
    %% 主分支
    M1[ ]:::hidden
    A1 --- M1
    M1 --> B1(基本概念)
    M1 --> B2(事件的关系与运算)
    M1 --> B3(古典概型与几何概型)
    M1 --> B4(概率的定义与性质)
    M1 --> B5(条件概率)
    M1 --> B6(事件独立性)
    M1 --> B7(全概率公式与贝叶斯公式)

    %% B1: 基本概念 的分支
    M1_2[ ]:::hidden
    B1 --- M1_2
    M1_2 --> C1_1(随机试验)
    M1_2 --> C1_2("样本点、样本空间")
    M1_2 --> C1_4(随机事件)
    M1_2 --> C1_7(事件发生)
    
    %% C1_4: 随机事件的子节点
    M1_3[ ]:::hidden
    C1_4 --- M1_3
    M1_3 --> C1_3(基本事件)
    M1_3 --> C1_5(不可能事件)
    M1_3 --> C1_6(必然事件)

    %% B2: 事件的关系与运算 的分支
    M2_2[ ]:::hidden
    B2 --- M2_2
    M2_2 --> C2_1("包含、相等、和差、互斥、对立")
    M2_2 --> C2_2("交换律、结合律、分配律、对偶律")

    %% B4: 概率的定义与性质 的分支
    M4_2[ ]:::hidden
    B4 --- M4_2
    M4_2 --> C4_1("统计定义、公理化定义")
    M4_2 --> C4_2("非负性、规范性、有限可加性")
    M4_2 --> C4_3("加法公式、减法公式")

    %% B5: 条件概率 的分支
    B5 --> C5_1(乘法公式)

    %% B6: 事件独立性 的分支
    M6_2[ ]:::hidden
    B6 --- M6_2
    M6_2 --> C6_1(两个事件)
    M6_2 --> C6_2(多个事件)

    %% B7: 全概率公式与贝叶斯公式 的分支
    M7_2[ ]:::hidden
    B7 --- M7_2
    M7_2 --> C7_1(完备事件组)
    M7_2 --> C7_2(抽签原理)

1-1. 随机事件与样本空间

内容比较简单，略过

1-2. 随机事件与样本空间

选择题考了要能知道是在说什么事件并且要知道公式

  • 差事件: \(A - B = A\overline{B}\) 表示A发生B不发生

  • 互斥事件也就是互不相容事件

  • 互逆事件也就是对立事件

  • 交换律: \(A \cup B = B \cup A\)，\(A \cap B = B \cap A\)

  • 结合律: \(A \cup (B \cup C) = (A \cup B) \cup C\)，\(A \cap (B \cap C) = (A \cap B) \cap C\)

  • 分配律: \(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\)，\(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\)

例题：设 \(A,B\) 是两个随机事件，则 \((A \cup B)(\overline{A} \cup \overline{B}) =\) 点击查看答案\(A \overline{B} + \overline{A} B\) 点击跳转到视频讲解链接

  • 对偶律(德摩根律): \(\overline{A \cup B} = \overline{A} \cap \overline{B}\), \(\overline{A \cap B} = \overline{A} \cup \overline{B}\) ，简单来讲就是长横变短横，交和并互化

例题：以 \(A\) 表示事件”甲产品畅销，乙产品滞销”，则其对立事件 \(\overline{A}\) 为 点击查看答案D

（A）甲产品畅销，乙产品滞销； （B）甲、乙两种产品均畅销； （C）甲产品滞销； （D）甲产品滞销或乙产品畅销

点击跳转到视频讲解链接

1-3. 古典概型

古典概型简单来讲就是样本空间中的样本点出现的可能性相同

置球入盒模型，建议看视频讲解，我觉得很重要 点击跳转到视频讲解链接

1-4. 几何概型

几何概型简单来讲就是把古典概型扩展了一下，将等可能事件的概念从有限到无限延伸

例题：若在区间(0,1)内任取两个数，则事件”两数之和小于 \(\frac{6}{5}\)” 发生的概率为 点击查看答案\(\frac{17}{25}\)

点击跳转到视频讲解链接

1-5. 概率的概念和基本性质

概率论的基本功，要掌握

例题：如果事件 \(A\) 与 \(B\) 同时发生的概率为 \(P(AB) = 0\) ，则 点击查看答案D

（A）\(A\) 与 \(B\) 互斥 （B）\(AB\) 是不可能事件 （C）\(P(A) = 0 \text{ 或 } P(B) = 0\) （D）\(A\) 与 \(B\) 可能同时发生

点击跳转到视频讲解链接

不要想当然的以为AB是不可能事件，概率为0的事件也会发生，概率为1的事件也有可能不发生，一般来说，概率推事件是不对的

  • 有限可加性：若事件 \(A_1, A_2, \dots, A_n\) 两两互斥，则 \(P\left(\bigcup_{i=1}^{n} A_i\right) = \sum_{i=1}^{n} P(A_i)\)

  • 减法公式：对于任意两个随机事件 \(A\) 和 \(B\) ，有 \(P(A - B) = P(A) - P(AB)\)

  • 加法公式：对于任意两个随机事件 \(A\) 和 \(B\) ，有 \(P(A + B) = P(A) + P(B) - P(AB)\)

例题：试比较 \(P(A), P(AB), P(A+B), P(A) + P(B)\) 的大小 点击查看答案\(P(AB) \le P(A) \le P(A+B) \le P(A) + P(B)\)

点击跳转到视频讲解链接

例题：\(A\) , \(B\) 是两随机事件，\(P(AB) = P(\overline{A} \ \overline{B}), \quad P(A) = p\)，则 \(P(B)\) = 点击查看答案\(1 - p\)

点击跳转到视频讲解链接

1-6. 条件概率

同样比较基础，也得会

  • 条件概率定义：设 A, B 为两个事件，若 P(B) > 0，称 \(P(A|B) = \frac{P(AB)}{P(B)}\) 为事件 B 发生条件下事件 A 发生的条件概率。

  • 可列可加性：对两两互斥的事件列 \(A_1, A_2, \ldots, A_n, \ldots\), 有 \(P\left(\bigcup_{i=1}^{\infty} A_i \mid B\right) = \sum_{i=1}^{\infty} P(A_i \mid B)\)

  • 加法公式和减法公式和上一节的一样，但是要带上 \(|\) 下面的字母

例题：设 A, B 是两随机事件，\(P(A) = 0.4, P(B) = 0.3, P(A|B) = 0.5\)，则 \(P(A \cup B)\) = 点击查看答案\(0.55\)

点击跳转到视频讲解链接

例题：某人忘记了电话号码的最后一个数字，因此他随意地拨号。

  1. 求他不超过三次能打通所需电话的概率 点击查看答案\(\frac{3}{10}\)

  2. 若已知最后一个数字是奇数，求他不超过三次能打通所需电话的概率 点击查看答案\(\frac{3}{5}\)

点击跳转到视频讲解链接

1-7. 事件间的独立性

二级结论比较多

  • 设 A 与 B 是两事件，如果满足等式 \(P(AB) = P(A)P(B)\)，称事件 A 与 B 相互独立，简称 A, B 独立。

  • 若事件 A 与事件 B 相互独立，则 \(A\) 与 \(\overline{B}\)，\(\overline{A}\) 与 \(B\)，\(\overline{A}\) 与 \(\overline{B}\) 亦相互独立。

  • 若不说明 \(0 < P(A) < 1, 0 < P(B) < 1\)，则 A 与 B 是否独立和 A 与 B 是否互斥无必然联系。在概率不为 0 或 1 的情况下，独立一定不互斥，互斥一定不独立

例题：设 \(A\) 与 \(B\) 互斥（互不相容），则下列结论中正确的是 点击查看答案D

A. \(\overline{A}\) 与 \(\overline{B}\) 互斥 B. \(\overline{A}\) 与 \(\overline{B}\) 相容 C. \(A\) 与 \(B\) 不独立 D. \(P(A\overline{B}) = P(A)\)

点击跳转到视频讲解链接

  • 三个事件的独立性：称事件 \(A, B, C\) 两两独立，如果

\[ \begin{cases} P(AB) = P(A)P(B) \\\\ P(BC) = P(B)P(C) \\\\ P(AC) = P(A)P(C) \end{cases} \]

进一步如果满足等式 \(P(ABC) = P(A)P(B)P(C)\)，则称事件 \(A, B, C\) 相互独立

注：相互独立的随机事件 \(A_1, A_2, \dots, A_n\) 中，任何一部分事件的和、差、积、逆运算结果，都与另一部分独立。

例如 \(\overline{A \cup B}\) 与 \(C\)，\(A - B\) 与 \(C\)，\(A\) 与 \(BC\)，他们都是相互独立的

1-8. 全概率公式和贝叶斯公式

高中学过，直接看题目

例题：某人到武汉参加会议，他乘火车、轮船、汽车或飞机去的概率分别为0.2，0.1，0.3和0.4。如果他乘火车、轮船、汽车前去，迟到的概率分别为 \(\frac{1}{3}\)，\(\frac{1}{12}\)，\(\frac{1}{4}\)，乘飞机不会迟到。结果他迟到了，求他是乘汽车去的概率。点击查看答案\(\frac{1}{2}\)

点击跳转到视频讲解链接

例题：将两信息分别为 \(A,B\) 发送出去，接收站收到时，\(A\) 被误收作 \(B\) 的概率为0.04，而 \(B\) 被误收作 \(A\) 的概率为0.07，信息 \(A\) 与信息 \(B\) 传送频繁程度为3:2。若已知接收到的信息是 \(A\)，求原发信息也是 \(A\) 的概率。点击查看答案\(\frac{144}{151}\approx 0.9536\)

点击跳转到视频讲解链接

第二章-随机变量及其分布

%%{init: {'flowchart': {'curve': 'stepAfter'}}}%%
graph LR
    %% 定义隐藏节点样式
    classDef hidden fill:none,stroke:none,width:0px,height:0px
    
    A2(随机变量及其分布)

    %% 主分支
    N1[ ]:::hidden
    A2 --- N1
    N1 --> D1(随机变量)
    N1 --> D2(分布函数)
    N1 --> D3(常见离散型随机变量分布)
    N1 --> D4(常见连续型随机变量分布)
    N1 --> D5("随机变量函数 Y=g(X) 的分布")

    %% D1: 随机变量 的分支
    N2[ ]:::hidden
    D1 --- N2
    N2 --> E1_1(离散型)
    N2 --> E1_2(连续型)
    N2 --> E1_3(非离散非连续型)
    
    E1_1 --> F1_1(分布律)
    E1_2 --> F1_2(概率密度)

    %% D2: 分布函数 的分支
    N3[ ]:::hidden
    D2 --- N3
    N3 --> E2_1(定义)
    N3 --> E2_2(性质)

    %% D3: 常见离散型随机变量分布 的分支
    N4[ ]:::hidden
    D3 --- N4
    N4 --> E3_1(二项分布)
    N4 --> E3_2(0-1分布)
    N4 --> E3_3(泊松分布)
    N4 --> E3_4(几何分布)
    N4 --> E3_5(超几何分布)

    E3_3 --> F3_1(泊松定理)

    %% D4: 常见连续型随机变量分布 的分支
    N5[ ]:::hidden
    D4 --- N5
    N5 --> E4_1(均匀分布)
    N5 --> E4_2(指数分布)
    N5 --> E4_3(正态分布)

    %% D5: 随机变量函数的分布 的分支
    N6[ ]:::hidden
    D5 --- N6
    N6 --> E5_1(离散型X)
    N6 --> E5_2(连续型X)

    N7[ ]:::hidden
    E5_2 --- N7
    N7 --> F5_1(分布函数法)
    N7 --> F5_2(公式法)

2-1. 随机变量

内容比较简单，略过

2-2. 分布函数

所有随机变量都有分布函数，连续型随机变量的分布函数是处处连续的，离散型随机变量的分布函数的有跳跃间断点的

  • 分布函数定义：设 \(X\) 是一个随机变量， \(x\) 是任意实数，函数 \(F(x) = P\{X \le x\}, -\infty < x < +\infty\) 称为 \(X\) 的分布函数. 它表示 \(X\) 的取值落在实数 \(x\) 左侧的概率，所有的随机变量 \(X\) 都有分布函数 \(F(x)\)

  • \(P\{X \le a\} = F(a)\); \(P\{X < a\} = F(a-0)\);

  • 分布函数 \(F(X)\) 的基本性质：

  1. 非负性：\(0 \le F(x) \le 1\).
  2. 单调性：\(F(x)\) 是 \(x\) 的单调不减函数，即对 \(\forall x_1 < x_2\)，有 \(F(x_1) \le F(x_2)\).
  3. 规范性：\(F(-\infty) = \lim_{x \to -\infty} F(x) = 0\), \(F(+\infty) = \lim_{x \to +\infty} F(x) = 1\).
  4. 右连续性：\(F(x_0) = F(x_0 + 0)\).

2-3. 离散型随机变量

离散型随机变量就不讲了，比较简单，要记住的是：只有离散型才有分布律，有分布律的一定是离散型

2-4. 二项分布 \(X \sim B(n, p)\)

高中学过，这里简单回顾一下

定义：随机变量 \(X\) 表示 \(n\) 重伯努利试验中事件 \(A\) 发生的次数。记每次试验中事件 \(A\) 发生的概率为 \(p\)，则 \(X\) 的分布律为

\(P\{X = k\} = C_n^k p^k (1-p)^{n-k}, (k = 0, 1, ..., n)\)

其中 \(0<p<1\)，则称 \(X\) 服从参数为 \(n, p\) 的二项分布，记为 \(X \sim B(n, p)\)

2-5. \(0-1\) 分布、几何分布 \(X \sim Ge(p)\)

0-1分布就是随机变量X只能取0，1的特殊二项分布 几何分布就是前面几次试验都失败，最后一次成功的二项分布

几何分布公式：\(P\{X = k\} = (1-p)^{k-1}p, (k = 1, 2, ...)\)

其中 \(0<p<1\)，则称 \(X\) 服从几何分布，记作 \(X \sim Ge(p)\)

2-6. 泊松分布 \(X \sim P(\lambda)\)

这个考点题目一般会很直白的说出来X服从泊松分布

泊松分布 \(P(\lambda)\)：设随机变量 \(X\) 所有可能取的值为 \(0, 1, 2, ...\)，其分布律为

\(P\{X = k\} = \frac{\lambda^k e^{-\lambda}}{k!}, (k = 0, 1, 2, ...)\)

当二项分布中 \(n\) 很大 \(p\) 很小时，二项分布可以近似成泊松分布，此时 \(\lambda = np\)，注意，要题目说了才能这样近似

2-7. 超几何分布 \(X \sim H(n, M, N)\)

高中学过，简单回顾下

超几何分布的分布律：\(P\{X = k\} = \frac{C_M^k C_{N-M}^{n-k}}{C_N^n}, k = max\{0, n - N + M\}, ..., min\{n, M\}\)

2-8. 连续型随机变量

只有连续型随机变量才有概率密度 \(f(x)\) ,有概率密度 \(f(x)\) 的一定是连续型随机变量

\(F(x) = \int_{-\infty}^{x} f(t) dt\)，其中 \(f(x)\) 不一定要连续，可积就行了，但 \(F(X)\) 必须要处处连续

\(P\{X = a\} = 0，P\{a < X \le b\} = P\{a \le X < b\} = P\{a \le X \le b\} = P\{a < X < b\}\).连续型随机变量不用在意等号

概率密度 \(f(x)\) 的性质：

  • 非负性：\(f(x) \ge 0\).
  • 规范性：\(\int_{-\infty}^{+\infty} f(x) dx = 1\).
  • 对于任意实数 \(a, b\)， \(a \le b\)，有 \(P\{a < X \le b\} = F(b) - F(a) = \int_{a}^{b} f(x) dx\).
  • 若 \(f(x)\) 在点 \(x\) 连续，则有 \(F'(x) = f(x)\).

2-9. 均匀分布 \(X \sim U(a,b)\)

均匀分布的概率密度：\(f(x) = \begin{cases} \frac{1}{b-a}, & a < x < b, \\\\ 0, & 其他, \end{cases}\)

均匀分布的分布函数：\(F(x) = \begin{cases} 0, & x < a, \\\\ \frac{x-a}{b-a}, & a \le x < b, \\\\ 1, & x \ge b. \end{cases}\)

计算技巧：

假设 \(X \sim U(-1, 2)\) , 求 \(P\{X \ge 0\}\)

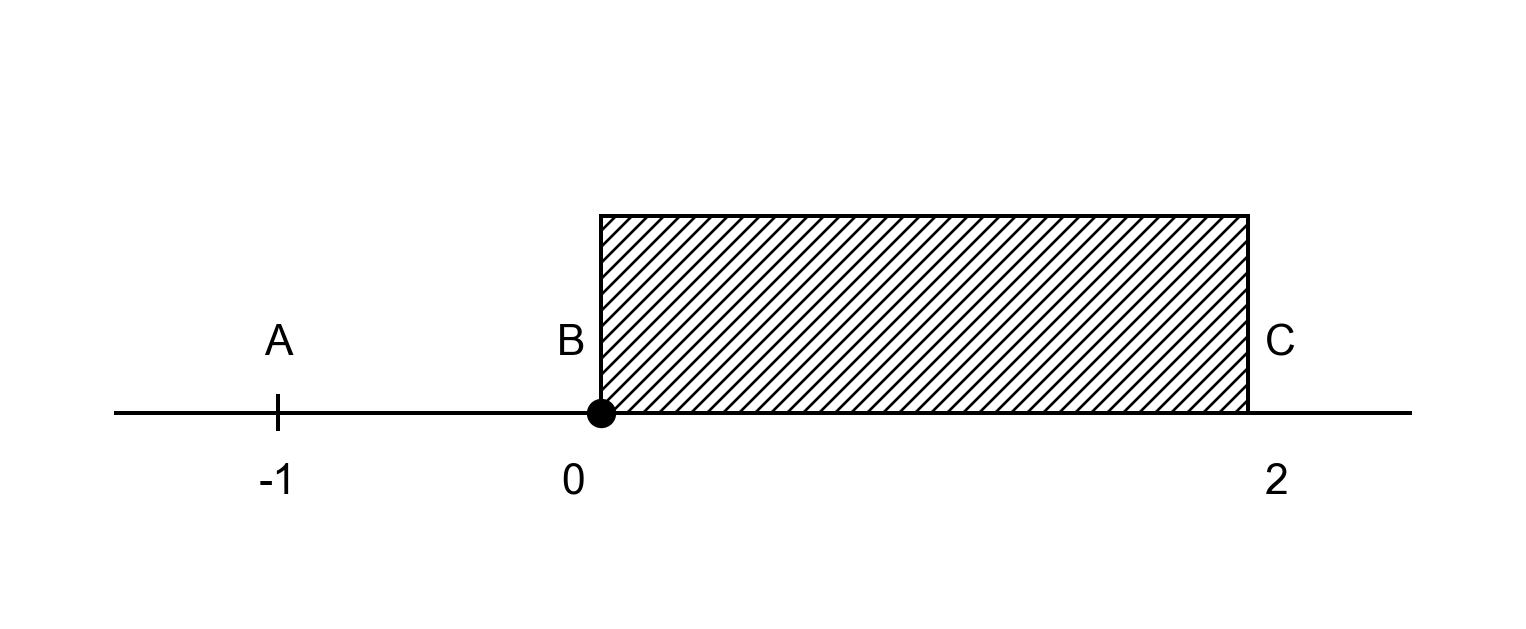
\(P\{X \ge 0\} = \frac{L_{BC}}{L_{AC}} = \frac{2}{3}\)

2-11. 指数分布 \(X \sim E(\lambda)\)

指数分布的概率密度：\(f(x) = \begin{cases} \lambda e^{-\lambda x}, & x > 0, \\\\ 0, & x \le 0, \end{cases}\)

指数分布的分布函数\(F(x) = \begin{cases} 1 - e^{-\lambda x}, & x \ge 0, \\\\ 0, & x < 0. \end{cases}\)

计算技巧：

当 \(a>0\) 且 \(X \sim E(\lambda)\) ， \(P\{X>a\} = 1 - P\{X \le a\} = 1 - F(a) = e^{-\lambda a}\) ，当 \(a<=0\) 时，可以直接得出 \(P\{X>a\} = 1\) , 因为是必然事件

2-12. 正态分布 \(X \sim N(\sigma, \mu^2)\)

正态分布的概率密度：\(f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}, -\infty < x < +\infty\)

\(Y = aX + b \sim N(a\mu + b, a^2\sigma^2), a \ne 0\) ，即正态随机变量的一次函数仍服从正态分布.

标准正态分布：

  1. 定义：当 \(\mu = 0, \sigma = 1\) 时，称 \(X\) 服从标准正态分布，记为 \(X \sim N(0,1)\)，其概率密度为 \(\varphi(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}, -\infty < x < +\infty\)，分布函数用 \(\Phi(x)\) 表示。

  2. 正态分布的标准化：

若 \(X \sim N(\mu, \sigma^2)\)，则 \(Z = \frac{X-\mu}{\sigma} \sim N(0,1)\)。于是有

\(F(x) = P\{X \le x\} = P\{\frac{X-\mu}{\sigma} \le \frac{x-\mu}{\sigma}\} = \Phi(\frac{x-\mu}{\sigma})\)

\(P\{a < X \le b\} = P\{\frac{a-\mu}{\sigma} < \frac{X-\mu}{\sigma} \le \frac{b-\mu}{\sigma}\} = \Phi(\frac{b-\mu}{\sigma}) - \Phi(\frac{a-\mu}{\sigma})\)

标准正态分布的性质：

  1. \(\Phi(-a) = 1 - \Phi(a), \forall a \in R\);
  2. \(\Phi(0) = \frac{1}{2}\);
  3. \(P\{|X| \le a\} = 2\Phi(a) - 1\), 其中 \(a > 0\)

2-13. 随机变量函数 \(Y = g(X)\) 分布

这一节好好看看视频，要自己动手算，点击跳转到视频讲解链接

第三章-多维随机变量及其分布

%%{init: {
  'flowchart': {
    'curve': 'stepAfter',
    'nodeSpacing': 20,
    'rankSpacing': 50,
    'padding': 10
  }
}}%%
graph LR
    %% 定义隐藏节点样式
    classDef hidden fill:none,stroke:none,width:0px,height:0px
    
    A3("多维随机变量及其分布")

    P1[ ]:::hidden
    A3 --- P1
    P1 --> H1("二维离散型")
    P1 --> H2("二维连续型")
    P1 --> H3("联合分布函数")
    P1 --> H4("独立性判别")
    P1 --> H5("二维随机变量函数的分布")

    %% H1: 二维离散型 的分支
    P2[ ]:::hidden
    H1 --- P2
    P2 --> I1_1("求联合分布律")
    P2 --> I1_2("求边缘分布律")
    P2 --> I1_3("求条件分布律")
    P2 --> I1_4("求概率")
    P2 --> I1_5("已知条件分布求联合分布")
    P2 --> I1_6("已知边缘分布和条件分布求联合分布")

    %% H2: 二维连续型 的分支
    P3[ ]:::hidden
    H2 --- P3
    P3 --> I2_1("已知联合概率密度")
    P3 --> I2_2("已知联合分布函数")
    P3 --> I2_3("利用充要条件")
    P3 --> I2_4("求边缘概率密度")
    P3 --> I2_5("求条件概率密度")
    P3 --> I2_6("求概率")
    
    P4[ ]:::hidden
    I2_4 --- P4
    P4 --> I2_7("求边缘概率密度")
    P4 --> I2_8("求条件概率")
    
    P3 --> J2_1("二维均匀分布")
    P3 --> J2_2("二维正态分布")

    %% H3: 联合分布函数 的分支
    P5[ ]:::hidden
    H3 --- P5
    P5 --> I3_1("已知联合分布律")
    P5 --> I3_2("已知联合概率密度")
    P5 --> I3_3("已知联合分布求边缘分布函数")

    %% H4: 独立性判别 的分支
    P6[ ]:::hidden
    H4 --- P6
    P6 --> I4_1("两个离散型")
    P6 --> I4_2("两个连续型")
    P6 --> I4_3("一个离散型一个连续型")

    %% H5: 二维随机变量函数的分布 的分支
    P7[ ]:::hidden
    H5 --- P7
    P7 --> I5_1("离散型 X Y")
    P7 --> I5_2("连续型 X Y")
    P7 --> I5_3("离散型X 和 连续型Y")
    P7 --> I5_4("X Y 独立")
    P7 --> I5_5("X Y 不独立")
    P7 --> I5_6("正态分布且独立")
    P7 --> I5_7("最大最小值分布")
    P7 --> I5_8("常见可加性分布")

    P8[ ]:::hidden
    I5_2 --- P8
    P8 --> J5_1("分布函数法")
    P8 --> J5_2("公式法")
    P8 --> J5_3("卷积公式法")

3-1. 多维随机变量及其分布函数

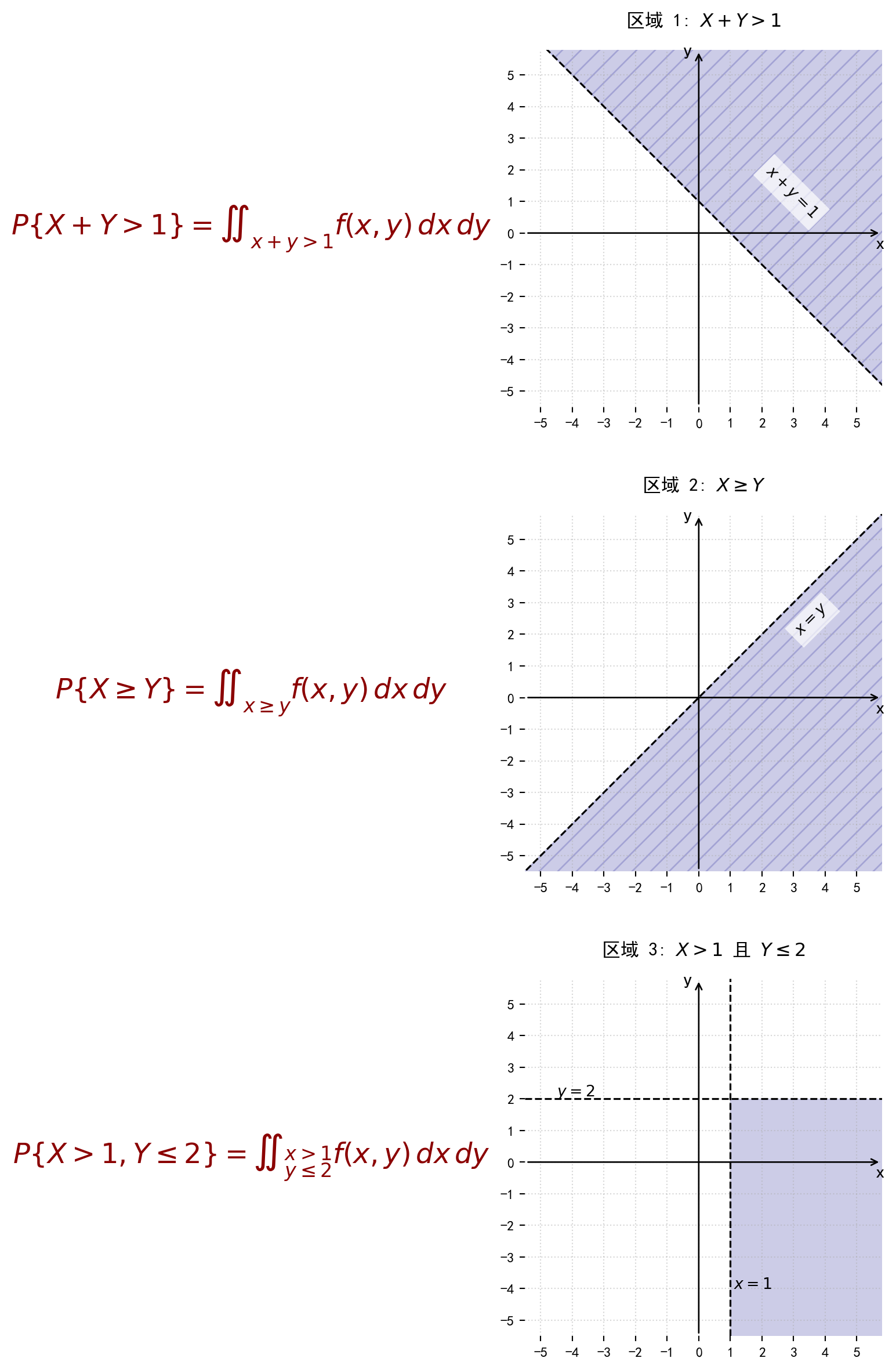
二维随机变量 \((X, Y)\) 的分布函数 \[ F(x, y) = P\{X \le x, Y \le y\} \] 它表示随机事件 \({X \le x} 和 {Y \le y}\) 同时发生的概率

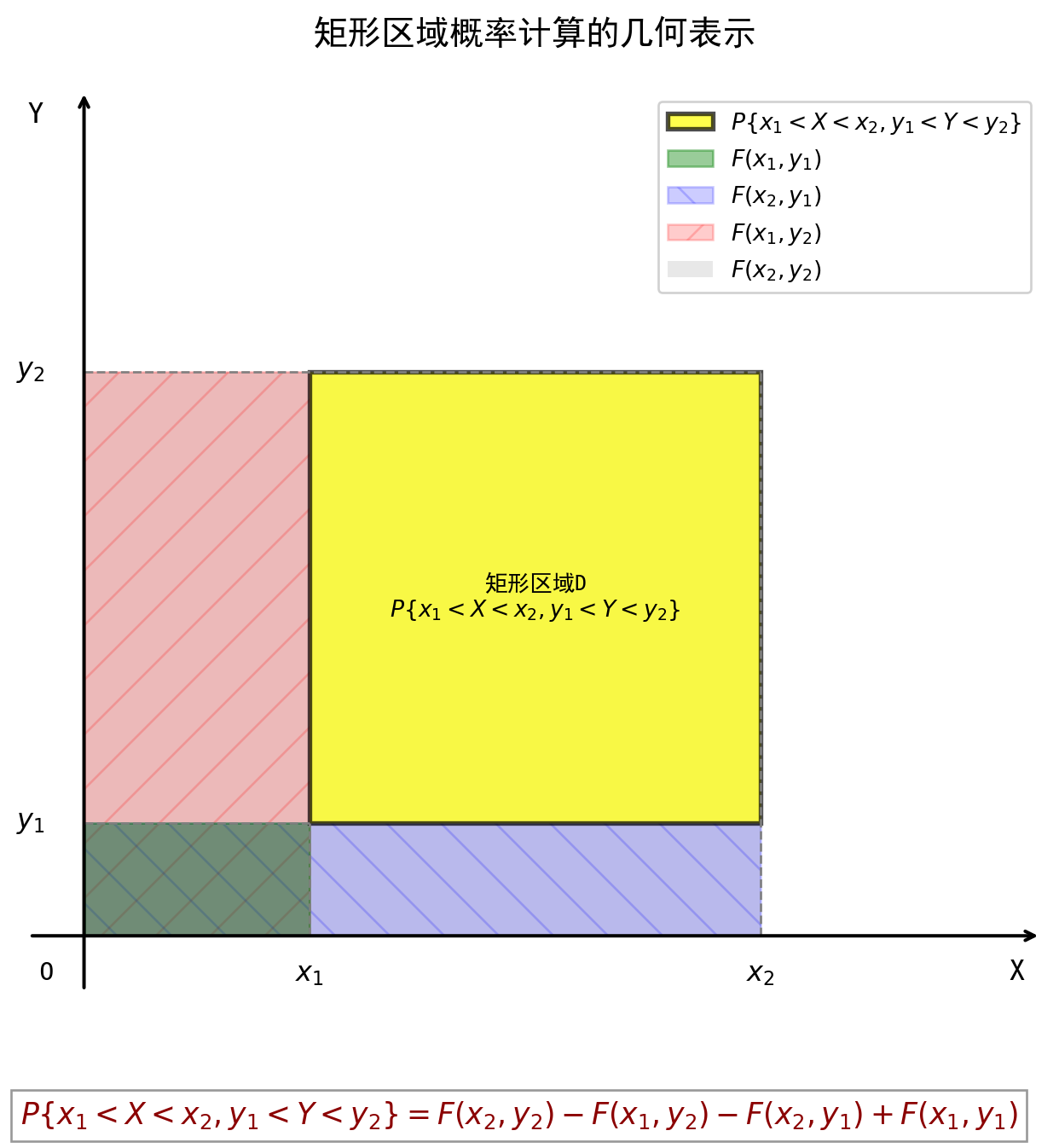
将二维随机变量 \((X, Y)\) 看成是平面上随机点的坐标，那么，分布函数 \(F(x, y)\) 在点 \((x, y)\) 处的函数值就是随机点 \((X, Y)\) 落在为顶点而位于直线 \(X = x\) 的左侧和直线 \(Y = y\) 的下方的无穷矩形区域内的概率。 如下图：

Figure 1

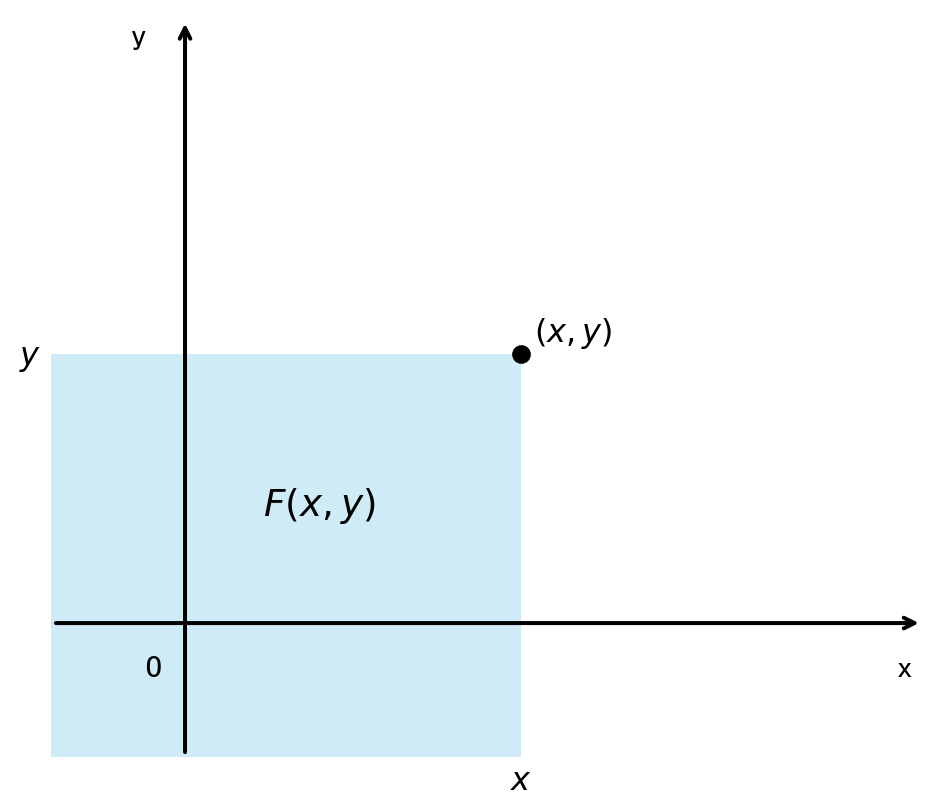
随机点 \((X, Y)\) 落在矩形区域 \(D = \{(x, y) | x_1 < X \le x_2, y_1 < Y \le y_2\}\) 内的概率为 \[ P\{x_1 < X \le x_2, y_1 < Y \le y_2\} = F(x_2, y_2) - F(x_1, y_2) - F(x_2, y_1) + F(x_1, y_1) \]

Figure 2

分布函数 \(F(X, Y)\) 的性质：

  • 规范性：对于任意固定的 \(y\)， \(F(-\infty, y) = \lim_{x \to -\infty} F(x, y) = 0\) ，对于任意固定的 \(x\)， \(F(x, -\infty) = \lim_{y \to -\infty} F(x, y) = 0\)， \(F(-\infty, -\infty) = 0\), \(F(+\infty, +\infty) = 1\) ，即 \(X\) 或者 \(Y\) 中只要有一个是负无穷，\(F(X,Y)\) 就为 \(0\) , 全为正无穷， \(F(X,Y)\) 才为1

  • 单调不减性：\(F(x, y)\) 关于变量 \(x\) 和 \(y\) 单调不减，即对于任意固定的 \(y\)，当 \(x_2 > x_1\) 时，\(F(x_2, y) \ge F(x_1, y)\)；对于任意固定的 \(x\)，当 \(y_2 > y_1\) 时，\(F(x, y_2) \ge F(x, y_1)\)

  • 右连续性：\(F(x, y)\) 关于变量 \(x\) 右连续，关于 \(y\) 也右连续，即 \(F(x+0, y) = F(x, y), F(x, y+0) = F(x, y)\)

边缘分布函数：\(F_X(x) = P\{X \le x\} = P\{X \le x, Y < +\infty\} = F(x, +\infty)\),即 \(F_X(x) = F(x, +\infty)\)，同理 \(F_Y(y) = F(+\infty, y)\)

如果 \(P\{X \le x, Y \le y\} = P\{X \le x\} \cdot P\{Y \le y\}\),即 \(F(x, y) = F_X(x) \cdot F_Y(y)\)，则称随机变量 \(X\) 和 \(Y\) 相互独立。

性质: 设 \(X_1, X_2, ..., X_n\) 相互独立，且 \(g_1(x), g_2(x), ..., g_n(x)\) 均为连续函数，则 \(g_1(X_1), g_2(X_2), ..., g_n(X_n)\) 也相互独立.(独立随机变量的连续函数也独立)

比如：\(X和Y\) 独立，则 \(X^2\) 和 \(e^Y\) 也独立

3-2. 二维离散型随机变量的分布和独立性

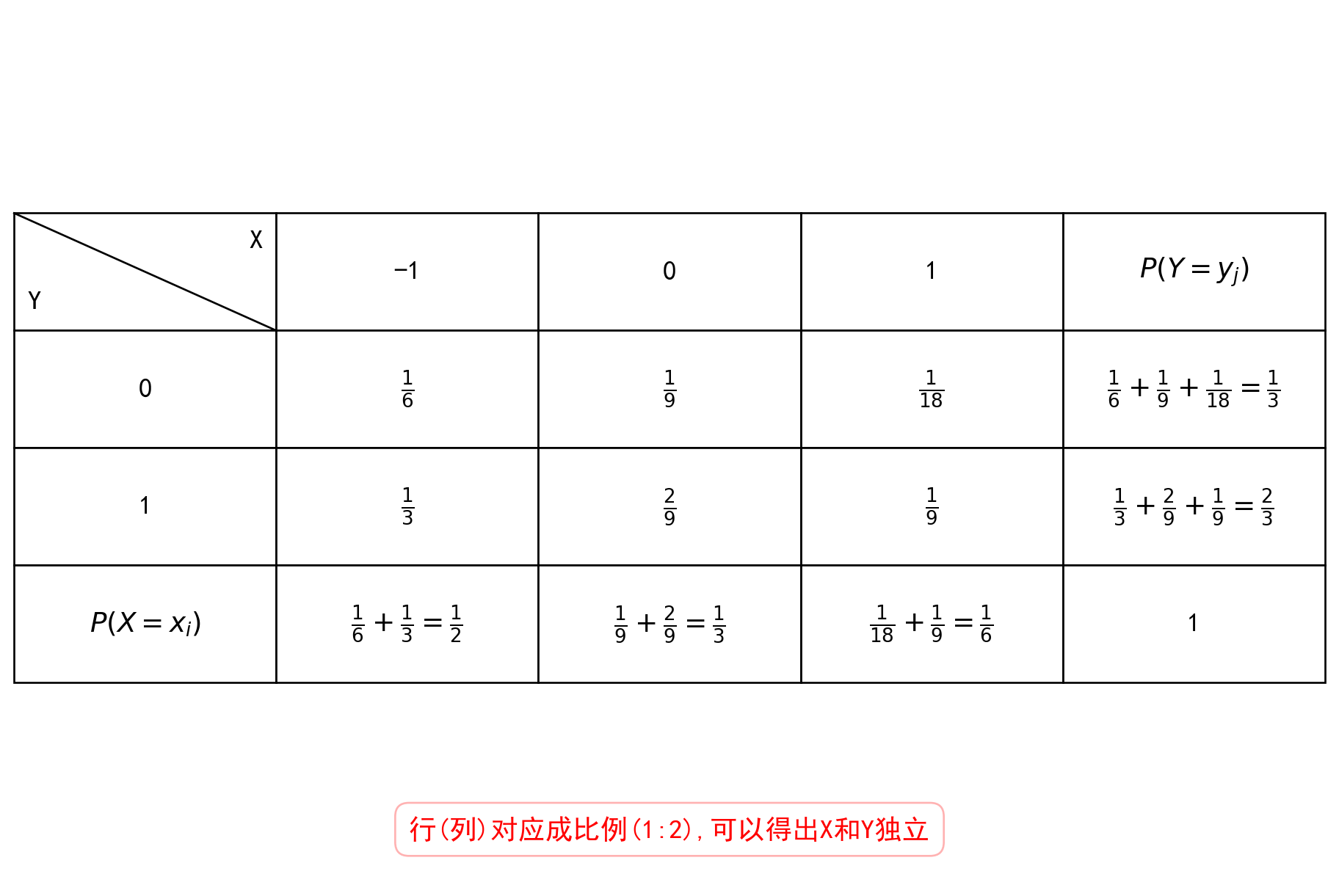
二维离散型随机变量的分布律 \(P(X = x_i, Y = y_j) = p_{ij}, i, j = 1, 2, ...\) ，表示 \(X = x_i, Y = y_j\) 同时发生的概率是 \(p_{ij}\) , 由概率定义有 \(p_{ij} \ge 0, \sum_{i=1}^{+\infty} \sum_{j=1}^{+\infty} p_{ij} = 1\).

二维离散型随机变量的分布函数 \(F(x, y) = P\{X \le x, Y \le y\} = \sum_{x_i \le x} \sum_{y_j \le y} p_{ij}\)

\(X\) 的边缘分布律为:\(P\{X = x_i\} = P\{X = x_i, Y < +\infty\} = \sum_{j=1}^{\infty} P\{X = x_i, Y = y_j\} = \sum_{j=1}^{\infty} p_{ij} = p_{i.}, i = 1, 2, ...\)

\(X\) 的边缘分布函数为: \(F_X(x) = P\{X \le x\} = \sum_{x_i \le x} P\{X \le x_i\} = \sum_{x_i \le x} p_{i.}\)

同理，\(Y\) 的边缘分布律为:

\(P\{Y = y_j\} = P\{X < +\infty, Y = y_j\} = \sum_{i=1}^{\infty} P\{X = x_i, Y = y_j\} = \sum_{i=1}^{\infty} p_{ij} = p_{.j}, j = 1, 2, ...\)

\(Y\) 的边缘分布函数为: \(F_Y(x) = P\{Y \le y\} = \sum_{y_j \le y} P\{Y = y_j\} = \sum_{y_j \le y} p_{.j}\)

条件分布率定义： 设 \((x, Y)\) 是二维离散型随机变量，对于固定的 \(j\)，若 \(P\{Y = y_j\} > 0\)

则称

\(P\{X = x_i | Y = y_j\} = \frac{P\{X = x_i, Y = y_j\}}{P\{Y = y_j\}} = \frac{p_{ij}}{p_{.j}}, i = 1, 2, ...\)

为在 \(Y = y_j\) 条件下随机变量 \(X\) 的条件分布律。

下面作图直观演示下边缘分布函数计算过程

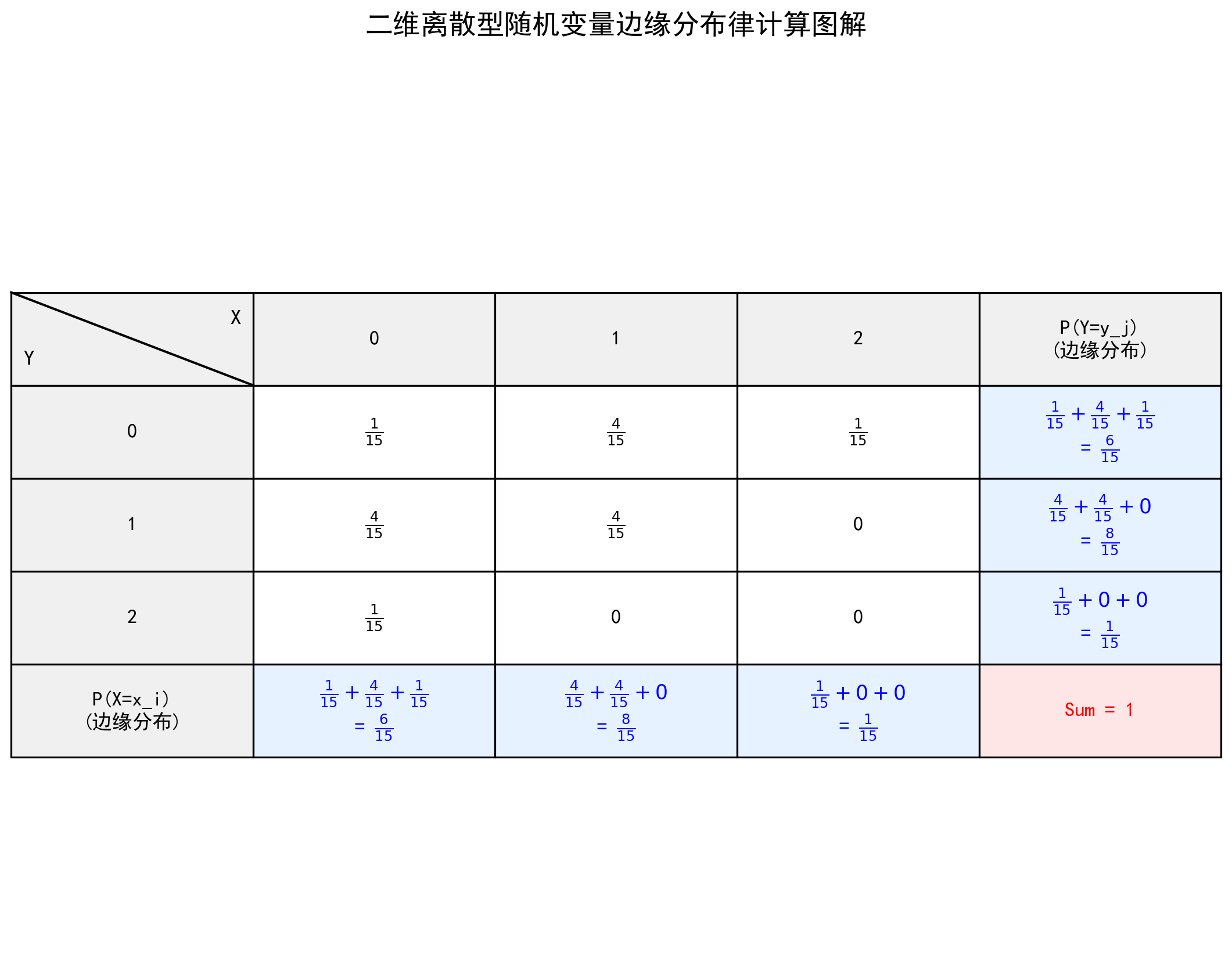
二维离散型随机变量 \(X\) 和 \(Y\) 独立的充要条件：

\(P\{X = x_i, Y = y_j\} = P\{X = x_i\} \cdot P\{Y = y_j\}, i, j = 1, 2, ...\)

即 \(p_{ij} = p_{i.} \cdot p_{.j}, (i, j = 1, 2, ...)\)

下面给出判断独立的小技巧：

  • 如果有一个\(P\{X = x_i, Y = y_j\} = 0\) , 那么就可以直接判断不独立

  • 如果分布律表格中的行(列)对应成比例，那么一定独立

3-3. 二维连续型随机变量的概念和性质

和一维概率密度函数 \(f(x)\) 的一样，二维连续型随机变量的概率密度函数 \(f(x,y)\) 同样也是 \(X\) 和 \(Y\) 都是连续型随机变量才存在

二维连续型随机变量的分布函数：\(F(x, y) = P\{X \le x, Y \le y\} = \int_{-\infty}^{x} \int_{-\infty}^{y} f(u, v) du dv\)

联合密度函数性质： \(\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(x, y) dxdy = 1\);

设 \(G\) 是 \(xOy\) 平面上任一区域，则点 \((X, Y)\) 落在 \(G\) 内的概率为

\(P\{(X, Y) \in G\} = \iint_{G} f(x, y) dxdy\).

若 \(f(x, y)\) 在点 \((x, y)\) 处连续，则有 \(f(x, y) = \frac{\partial^2 F(x,y)}{\partial x \partial y}\). 如果给出了 \(F(x,y)\) 一般情况下，\(F(x,y)\) 是连续的，那么可以直接求二阶偏导得到 \(f(x,y)\)

Figure 3: 多维随机变量的三个概率区域表示

3-4. 二维连续型随机变量求概率和分布函数

设二维随机变量 \((X,Y)\) 的密度函数为

\(f(x,y) = \begin{cases} Cxy, & 0 \le x \le 1, 0 \le y \le 1, \\ 0, & \text{其他}. \end{cases}\)

求: (I) 常数 \(C\); (II) \(P\{X+Y < 1\}\); (III) 联合分布函数 \(F(x,y)\).

(I)点击查看答案4

(II)点击查看答案 \(\frac{1}{6}\)

(III)点击查看答案\[F(x,y) = \begin{cases} 0, & x<0 \text{ 或 } y<0 \\ x^2y^2, & 0 \le x < 1, 0 \le y < 1 \\ x^2, & 0 \le x < 1, y \ge 1 \\ y^2, & 0 \le y < 1, x \ge 1 \\ 1, & x \ge 1, y \ge 1 \end{cases}\]

点击跳转到视频讲解链接

3-5. 边缘概率密度

\(X\) 的边缘分布函数 \(F_X(x) = F(x, +\infty) = \int_{-\infty}^{x} [\int_{-\infty}^{+\infty} f(x, y) dy] dx\)，其密度函数为 \(f_X(x) = F'_X(x) = \int_{-\infty}^{+\infty} f(x, y) dy\)

同理，\(Y\) 的边缘分布函数为 \(F_Y(y) = F(+\infty, y) = \int_{-\infty}^{y} [\int_{-\infty}^{+\infty} f(x, y) dx] dy\)，其密度函数为 \(f_Y(y) = F'_Y(y) = \int_{-\infty}^{+\infty} f(x, y) dx\)，分别称 \(f_X(x)\) 和 \(f_Y(y)\) 为 \((X, Y)\) 关于 \(X\) 和 \(Y\) 的边缘概率密度。

3-6. 条件概率密度与条件概率

设二维随机变量 \((X, Y)\) 的概率密度为 \(f(x, y)\). 若对于固定的 \(y\), \(f_Y(y) > 0\) 则称 \(f_{X|Y}(x|y) = \frac{f(x, y)}{f_Y(y)}\) 为在 \(Y = y\) 的条件下 \(X\) 的条件概率密度

若对于固定的 \(x\), \(f_X(x) > 0\), 则称 \(f_{Y|X}(y|x) = \frac{f(x, y)}{f_X(x)}\) 为在 \(X = x\) 的条件下 \(Y\) 的条件概率密度

\(P\{X \le x | Y = y\}\) = \(\int_{-\infty}^{x} f_{X|Y}(u|y) du\)

辨析：\(P\{X \le x | Y = y\}\) 和 \(P\{X \le x | Y > y\}\)

前者是条件概率密度，后者是条件概率

计算 \(P\{X \le x | Y = y\}\) 的步骤：

  1. 先求边缘密度：\(f_Y(y) = \int_{-\infty}^{+\infty} f(x,y) dx\)。

  2. 再求条件密度：\(f_{X|Y}(x|y) = \frac{f(x,y)}{f_Y(y)}\)

  3. 最后积分：\(P\{X \le x | Y = y\} = \int_{-\infty}^{x} f_{X|Y}(u|y) du\)

计算 \(P\{X \le x | Y > y\}\) 的步骤：

\(P\{X \le x | Y > y\} = \frac{P(X \le x, Y > y)}{P(Y > y)}\)

注意书写规范，在写条件概率密度函数的时候，一定要先注明：在 \(X = x(x的范围) or Y = y(y的范围)\) 的条件下，\(f_{Y|x}(y|x) = ...\) or \(f_{X|Y}(x|y) = ...\)

3-7. 二维连续型随机变量的独立性

对于二维连续型随机变量 \((X, Y)\)，则 \(X\) 与 \(Y\) 相互独立的充要条件是 \[f(x, y) = f_X(x) \cdot f_Y(y)\]

判读二维连续型随机变量的独立性的小技巧： 1. \(f(x,y)\) 的表达式中，可以拆成 \(g(x) \cdot h(y)\) 2. \(x\) 和 \(y\) 的范围互不影响，各自写各自的 只有同时满足条件1和2时，才能说 \(X\) 和 \(Y\) 独立

eg： \[f(x, y) = \begin{cases} \frac{1}{2}e^{-\frac{y}{2}}, & 0 < x < 1, y > 0 \\ 0, & \text{其他} \end{cases}\] 这里可以很明显的看出 \(f(x, y)\) 是变量可分离的，并且 \(x\) 和 \(y\) 的取值范围都不相干

\[f(x, y) = \begin{cases} 3e^{-(x+3y)}, & x > 0, y > 0, \\ 0, & \text{其他}, \end{cases}\] 同样的，\(3e^{-(x+3y)}\) 也可以拆成 \(g(x) \cdot h(y)\) 的形式并且 \(x\) 和 \(y\) 的取值范围都不相干

\[f(x, y) = \begin{cases} (x+1)(y+1), & 0 < x < 1, 0 < y < 1-x \\ 0, & \text{其他} \end{cases}\] 这个就不独立了，因为\(x\) 和 \(y\) 的取值范围有联系

3-8. 二维连续型随机变量综合题（练习）

设二维随机变量 \((X,Y)\) 具有概率密度

\[f(x,y) = \begin{cases} Ae^{-(x+y)}, & 0 < x < y \\ 0, & \text{其他} \end{cases}\]

试求：(1) 常数 \(A\); (2) \(P\{X+Y > 1, X < \frac{1}{2}\}\); (3) \(X,Y\) 的边缘概率密度 \(f_X(x), f_Y(y)\); (4) 条件概率密度 \(f_{Y|X}(y|x)\); (5) \(X\) 与 \(Y\) 是否独立?

点击跳转到视频链接

3-9. 二维均匀分布

\(f(x, y) = \begin{cases} \frac{1}{S_D}, & (x, y) \in D, \\ 0, & \text{其他}, \end{cases}\)

性质：若 \((X, Y)\) 在 \(D\) 上服从二维均匀分布，则对 \(D\) 内的任意子区域 \(G\)，有 \[P\{(X, Y) \in G\} = \frac{S_G}{S_D}\]

3-10. 二维正态分布

定义 若二维随机变量 \((X,Y)\) 的概率密度为

\(f(x, y) = \frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}} \exp\left\{-\frac{1}{2(1-\rho^2)} \left[\frac{(x-\mu_1)^2}{\sigma_1^2} - 2\rho\frac{x-\mu_1}{\sigma_1}\frac{y-\mu_2}{\sigma_2} + \frac{(y-\mu_2)^2}{\sigma_2^2}\right]\right\}\)

\((x, y) \in R^2\), 其中参数 \(\mu_1, \mu_2, \sigma_1, \sigma_2, \rho\) 均为常数，且 \(\sigma_1 > 0, \sigma_2 > 0, |\rho| < 1\), 则称 \((X,Y)\) 服从参数为 \(\mu_1, \mu_2, \sigma_1, \sigma_2\) 和 \(\rho\) 的二维正态分布，记作 \((X,Y) \sim N(\mu_1, \mu_2; \sigma_1^2, \sigma_2^2; \rho)\).

\(f(x,y)\) 的表达式太复杂了，不用背，了解即可

性质：

  1. 边缘分布是正态分布, 即 \(X \sim N(\mu_1, \sigma_1^2), Y \sim N(\mu_2, \sigma_2^2)\)

  2. \(X\) 与 \(Y\) 相互独立的充要条件为 \(\rho = 0\)

  3. \(X\) 与 \(Y\) 的非零线性组合 \(aX + bY\) 仍服从正态分布, 且 \(aX + bY \sim N(a\mu_1 + b\mu_2, a^2\sigma_1^2 + b^2\sigma_2^2 + 2ab\rho\sigma_1\sigma_2)\).

  4. 条件分布是正态分布

3-11. 二维随机变量函数分布（离散型）

Figure 4: 二维离散型随机变量分布律
  1. 求 \(U = X + Y\) 的概率分布. (2) 求 \(V = \min(X, Y)\) 的概率分布

点击跳转到视频讲解链接

3-12. 二维随机变量函数分布（连续型）

分布函数法：

分布函数 \(F_Z(z) = P\{Z \le z\} = P\{g(X, Y) \le z\} = \iint_{g(x, y) \le z} f(x, y) dxdy\), 将 \(z\) 取遍 \((-\infty, +\infty)\), 计算二重积分得 \(F_Z(z)\) 的函数表达式.

公式法：

设 \((X, Y)\) 的概率密度为 \(f(x, y)\)，则若 \(Z = g(X, Y)\) 可反解得 \(Y = h(X, Z)\)，则 \[f_Z(z) = \int_{-\infty}^{+\infty} \left|\frac{\partial h(x, z)}{\partial z}\right| f(x, h(x, z)) dx\]

同理，若 \(Z = g(X, Y)\) 可反解得 \(X = \varphi(Y, Z)\)，则 \[f_Z(z) = \int_{-\infty}^{+\infty} \left|\frac{\partial \varphi(y, z)}{\partial z}\right| f(\varphi(y, z), y) dy\]

分布函数法是通法，但计算量一般来讲比较大，公式法只有在能反解到X或Y的时候才能用，计算量一般比分布函数法小，考试的题目一般都能用公式法

3-13. 二维随机变量函数分布（正态）

当 \(X\) 和 \(Y\) 均服从正态分布且相互独立, \(X \sim N(\mu_1, \sigma_1^2)\), \(Y \sim N(\mu_2, \sigma_2^2)\), \(Z = aX + bY\)，可以直接得到 \(Z \sim N(a\mu_1 + b\mu_2, a^2\sigma_1^2 + b^2\sigma_2^2)\)，那么就可以得到 \(f(z) =\)

\(\frac{1}{\sqrt{2\pi(a^2\sigma_1^2 + b^2\sigma_2^2)}} e^{-\frac{(z - (a\mu_1 + b\mu_2))^2}{2(a^2\sigma_1^2 + b^2\sigma_2^2)}}\)

3-14. 最大最小值分布

设 \(X_1, X_2, ..., X_n\) 是相互独立的随机变量，分布函数分别为 \(F_{X_1}(x), F_{X_2}(x), ..., F_{X_n}(x)\)，则 \(U = \max(X_1, X_2, ..., X_n)\) 的分布函数为

\(F_{\max}(z) = F_{X_1}(z)F_{X_2}(z)...F_{X_n}(z)\)

推导过程：

\(U = \max\{X_1, ..., X_n\}\)

\(F_U(z) = P\{U \le z\} = P\{\max\{X_1, ..., X_n\} \le z\}\)

\(= P\{X_1 \le z, X_2 \le z, ..., X_n \le z\}\)

\(= P\{X_1 \le z\}P\{X_2 \le z\} ... P\{X_n \le z\}\)

\(= F_{X_1}(z) F_{X_2}(z) ... F_{X_n}(z)\)

\(V = \min(X_1, X_2, ..., X_n)\) 的分布函数为

\(F_{\min}(z) = 1 - [1 - F_{X_1}(z)][1 - F_{X_2}(z)]...[1 - F_{X_n}(z)]\)

特别地，当 \(X_1, X_2, ..., X_n\) 相互独立且 \(X_i \sim F(x)\) 时有:

\(F_{\max}(z) = [F(z)]^n\), \(F_{\min}(z) = 1 - [1 - F(z)]^n\)

推导过程：

\(F_V(z) = P\{\min\{X_1, X_2, ..., X_n\} \le z\}\)

\(= 1 - P\{\min\{X_1, X_2, ..., X_n\} > z\}\)

\(= 1 - P\{X_1 > z, X_2 > z, ..., X_n > z\}\)

\(= 1 - P\{X_1 > z\}P\{X_2 > z\} ... P\{X_n > z\}\)

\(= 1 - [1 - F_{X_1}(z)][1 - F_{X_2}(z)] ... [1 - F_{X_n}(z)]\)

第四章-数字特征

%%{init: {'flowchart': {'curve': 'stepAfter'}}}%%
graph LR
    %% 定义隐藏节点样式
    classDef hidden fill:none,stroke:none,width:0px,height:0px
    
    A1(数字特征)

    %% A1: 主分支
    N1[ ]:::hidden
    A1 --- N1
    N1 --> B1("求数学期望、方差")
    N1 --> B2(求协方差与相关系数)

    %% B1: 分支
    N2[ ]:::hidden
    B1 --- N2
    N2 --> C1(一维)
    N2 --> C2(二维)
    N2 --> C3(运算性质)
    N2 --> C4(常用分布的期望和方差)

    %% C1: 一维的分支
    N3[ ]:::hidden
    C1 --- N3
    N3 --> D1(离散型X及其函数)
    N3 --> D2(连续型X及其函数)

    %% C2: 二维的分支
    N4[ ]:::hidden
    C2 --- N4
    N4 --> D3("离散型 (X, Y) 及其函数")
    N4 --> D4("连续型 (X, Y) 及其函数")
    N4 --> D5("max {X, Y}, min {X, Y} 的期望")

    %% B2: 协方差分支
    N5[ ]:::hidden
    B2 --- N5
    N5 --> D6(判别X和Y是否相关)

4-1. 数学期望

离散型数学期望：

若级数 \(\sum_{k=1}^{\infty} x_k p_k\) 绝对收敛，则称该级数为 \(X\) 的数学期望，记为 \(EX\) \[ EX = \sum_{k=1}^{\infty} x_k p_k \] 否则，则 \(X\) 的数学期望不存在

连续型数学期望：

若 \(\int_{-\infty}^{+\infty} |x| f(x) dx < +\infty\) ，则称 \[ EX = \int_{-\infty}^{+\infty} x f(x) dx \] 为 \(X\) 的数学期望，否则，则 \(X\) 的数学期望不存在

一维随机变量的函数 \(Y = g(X)\) 的期望:

离散型： \[ EY = E[g(X)] = \sum_{k=1}^{\infty} g(x_k) p_k \]

连续型： \[ EY = E[g(X)] = \int_{-\infty}^{+\infty} g(x) f(x) dx \]

数学期望的性质：

  1. \(E(C) = C\) (其中 \(C\) 为常数)

  2. \(E(X + C) = E(X) + C\)

  3. \(E(CX) = CE(X)\)

  4. \(E(X \pm Y) = E(X) \pm E(Y)\)

  5. 设 \(X, Y\) 相互独立，则 \(E(XY) = EXEY\)

4-2. 二维随机变量函数的期望

二维随机变量函数 \(Z = g(X,Y)\) 的期望

离散型：

\[ EZ = E[g(X, Y)] = \sum_{j=1}^{\infty} \sum_{i=1}^{\infty} g(x_i, y_i) p_j \]

连续型：

\[ EZ = E[g(X, Y)] = \iint_{-\infty}^{+\infty} g(x, y) f(x, y) dxdy \]

4-3. 方差

定义: 设 \(X\) 为一随机变量，若 \(E(X - EX)^2\) 存在，则称 \(E(X - EX)^2\) 为 \(X\) 的方差，记为 \(DX\)，即

\(DX = E(X - EX)^2\)

称 \(\sqrt{DX}\) 为 \(X\) 的标准差. 易得计算公式 \(DX = EX^2 - (EX)^2\). 显然 \(DX \ge 0\).

计算时，\(DX = EX^2 - (EX)^2\) 这个公式用的最多

方差的性质:

  1. \(D(C) = 0\) (其中 \(C\) 为常数);

  2. \(D(X + C) = DX\)

  3. \(D(CX) = C^2DX\)

  4. 设 \(X, Y\) 相互独立，则 \(D(X \pm Y) = DX + DY\)(这里注意和期望的性质区分，\(E(X \pm Y) = E(X) \pm E(Y)\) 是通用的，不管 \(X 和 Y\) 是否独立)

  5. \(DX = 0\) 的充要条件是 \(P\{X = EX\} = 1\)

4-4. 常见分布的期望和方差

分布类型 分布律或概率密度 期望 方差
0-1 分布 \(p_k = P\{X=k\} = p^k q^{1-k} \quad (q=1-p), (k=0,1)\) \(p\) \(pq\)
二项分布 \(p_k = P\{X=k\} = C_n^k p^k q^{n-k}\)
\((q=1-p), (k=0,1,\dots,n)\)		 \(np\) \(npq\)
泊松分布 \(p_k = P\{X=k\} = \frac{\lambda^k}{k!} e^{-\lambda} \quad (k=0,1,2\dots)\) \(\lambda\) \(\lambda\)
均匀分布 \(f(x) = \begin{cases} \frac{1}{b-a}, & a < x < b \\ 0, & \text{其他} \end{cases}\) \(\frac{a+b}{2}\) \(\frac{(b-a)^2}{12}\)
正态分布 \(f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \quad (-\infty < x < +\infty, \sigma > 0)\) \(\mu\) \(\sigma^2\)
指数分布 \(f(x) = \begin{cases} \lambda e^{-\lambda x}, & x > 0 \\ 0, & x \le 0 \end{cases}\) \(\frac{1}{\lambda}\) \(\frac{1}{\lambda^2}\)
\(\chi^2\) 分布 \(X_1, X_2, \dots, X_n\) 相互独立，且都服从标准正态分布 \(N(0,1)\)
\(\chi^2 = X_1^2 + X_2^2 + \dots + X_n^2\)		 \(n\) \(2n\)
几何分布 \(p_k = P\{X=k\} = (1-p)^{k-1} p\)
\((k=1,2,\dots), 0 < p < 1\)		 \(\frac{1}{p}\) \(\frac{1-p}{p^2}\)

记住后做题直接用

4-5. 最大最小值分布的期望

回顾一下最大值最小值分布：

\[F_{\max}(z) = F_{X_1}(z)F_{X_2}(z)...F_{X_n}(z)\]

\[F_{\min}(z) = 1 - [1 - F_{X_1}(z)][1 - F_{X_2}(z)]...[1 - F_{X_n}(z)]\]

设随机变量 \(X\) 与 \(Y\) 相互独立，且都服从参数为 1 的指数分布，记 \(U = \max\{X, Y\}, V = \min\{X, Y\}\)，求 (I) \(EU\); (II) \(EV\); (III) \(EUV\)

点击跳转到视频讲解链接

结论：\(U + V = X + Y\), \(UV = XY\), \(U - V = |X - Y|\)

4-6. 切比雪夫不等式

定义：设随机变量具有数学期望 \(EX = \mu\)，方差 \(DX = \sigma^2\)，则对于任意正数 \(\epsilon\)，有下列切比雪夫不等式成立

\(P\{|X - EX| \ge \epsilon\} \le \frac{DX}{\epsilon^2}\) 或 \(P\{|X - EX| < \epsilon\} \ge 1 - \frac{DX}{\epsilon^2}\)

注意，这里只需要随机变量的数学期望和方差存在即可，并不需要该随机变量是正态随机变量

4-7. 协方差

定义：对于二维随机变量 \((X, Y)\)，若 \(E(X - EX)(Y - EY)\) 存在，则称它为 \(X\) 与 \(Y\) 的协方差，记为 \(Cov(X, Y)\)，即

\[ Cov(X, Y) = E(X - EX)(Y - EY) \]

易得计算公式 \[ Cov(X, Y) = EXY - EXEY \]

性质:

  1. \(Cov(X, Y) = Cov(Y, X)\);

  2. \(Cov(X, C) = 0\);

  3. \(Cov(aX, bY) = abCov(X, Y)\);

  4. \(Cov(X, X) = DX\)

  5. 设 \(X, Y\) 相互独立, 则 \(Cov(X, Y) = 0\)

  6. \(D(X \pm Y) = DX + DY \pm 2Cov(X, Y)\).

  7. \(Cov(X \pm Y, Z) = Cov(X, Z) \pm Cov(Y, Z)\);

性质1-5都可以由 \(Cov(X, Y) = EXY - EXEY\) 推出来

性质7可以用乘法分配律来理解,把协方差 \(Cov((a \pm b),c)\) 看作一种特殊的“乘法”, \((a \pm b)×c=ac \pm bc\)

举个例子来加深对以上性质的理解

设 \(X_1, X_2, X_3 \stackrel{iid}{\sim} N(0, 9) 且Cov(X_1 + 2X_2 - 3X_3, 2X_3 + 5)\)

由性质2: \(Cov(X, C) = 0\)，可以知道 \(Cov(X_1 + 2X_2 - 3X_3, 2X_3 + 5) = Cov(X_1 + 2X_2 - 3X_3, 2X_3)\)

由性质5：\(X, Y\) 相互独立, 则 \(Cov(X, Y) = 0\)，可以知道 \(Cov(X_1 + 2X_2 - 3X_3, 2X_3) = Cov(- 3X_3, 2X_3)\)

由性质3：\(Cov(aX, bY) = abCov(X, Y)\)，可以知道 \(Cov(- 3X_3, 2X_3) = -6Cov(X_3, X_3)\)

由性质4：\(Cov(X, X) = DX\)，可以知道 \(-6Cov(X_3, X_3) = -6D(X_3) = -6 × 9 = -54\)

例题：设随机变量 \((X, Y)\) 的密度函数 \(f(x, y) = \begin{cases} 3, & (x, y) \in G \\ 0, & \text{其他} \end{cases}\)，其中区域 \(G\) 由曲线 \(y = x^2\) 与 \(x = y^2\) 围成. 求 \(Cov(X, Y)\)

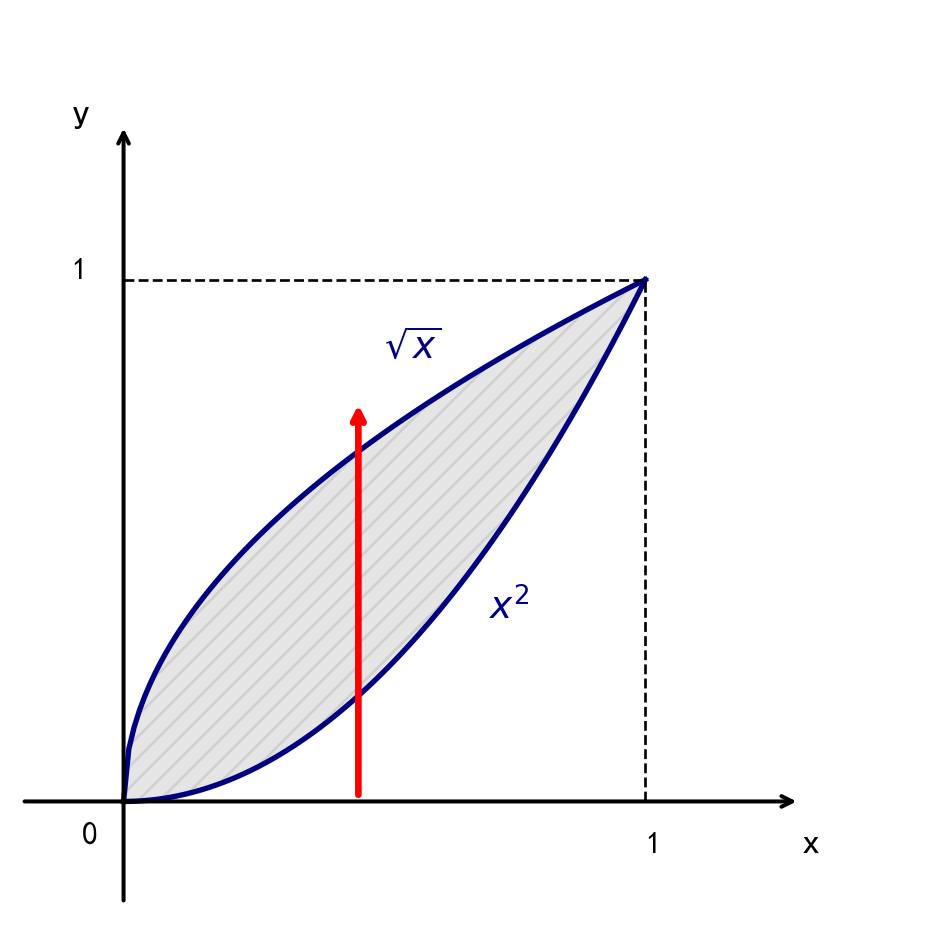
先列公式：\(Cov(X,Y) = EXY - EXEY\)

\(EXY = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} xy f(x, y) dx dy = \int_{0}^{1} dx \int_{x^2}^{\sqrt{x}} 3xy dy = \frac{1}{4}\)

算 \(EX\) 有技巧，不必走 \(f(x, y) \rightarrow f_X(x) \rightarrow EX\) 这个流程，可以把他当成二维随机变量，其中 \(X = g(X,Y)\)

\(EX = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} x f(x, y) dx dy = \int_{0}^{1} 3x dx \int_{x^2}^{\sqrt{x}} dy = \frac{9}{20}\)

由对称性，\(EY=EX=\frac{9}{20}\)

\(Cov(X,Y) = EXY - EXEY = \frac{1}{4} - \frac{9}{20} = \frac{19}{400}\)

4-8. 相关系数

定义对于二维随机变量 \((X, Y)\)，若 \(DX \ne 0, DY \ne 0\)，则称 \[ \rho_{XY} = \frac{Cov(X, Y)}{\sqrt{DX} \cdot \sqrt{DY}} \] 为 \(X\) 和 \(Y\) 的相关系数. 若 \(\rho_{XY} = 0\)，称 \(X\) 和 \(Y\) 不相关.

性质

  1. \(|\rho_{XY}| \le 1, \rho_{XY} = \rho_{YX}, \rho_{XX} = 1\);
  2. \(|\rho_{XY}| = 1\) 的充要条件是 \(X\) 与 \(Y\) 以概率 1 线性相关，即存在常数 \(a \ne 0\) 和 \(b\), 有 \(P\{Y = aX + b\} = 1\)
  3. \(|\rho_{XY}|\) 越接近于 1，表明 \(X\) 和 \(Y\) 的线性相关程度越大
Figure 5: 相关系数示意图

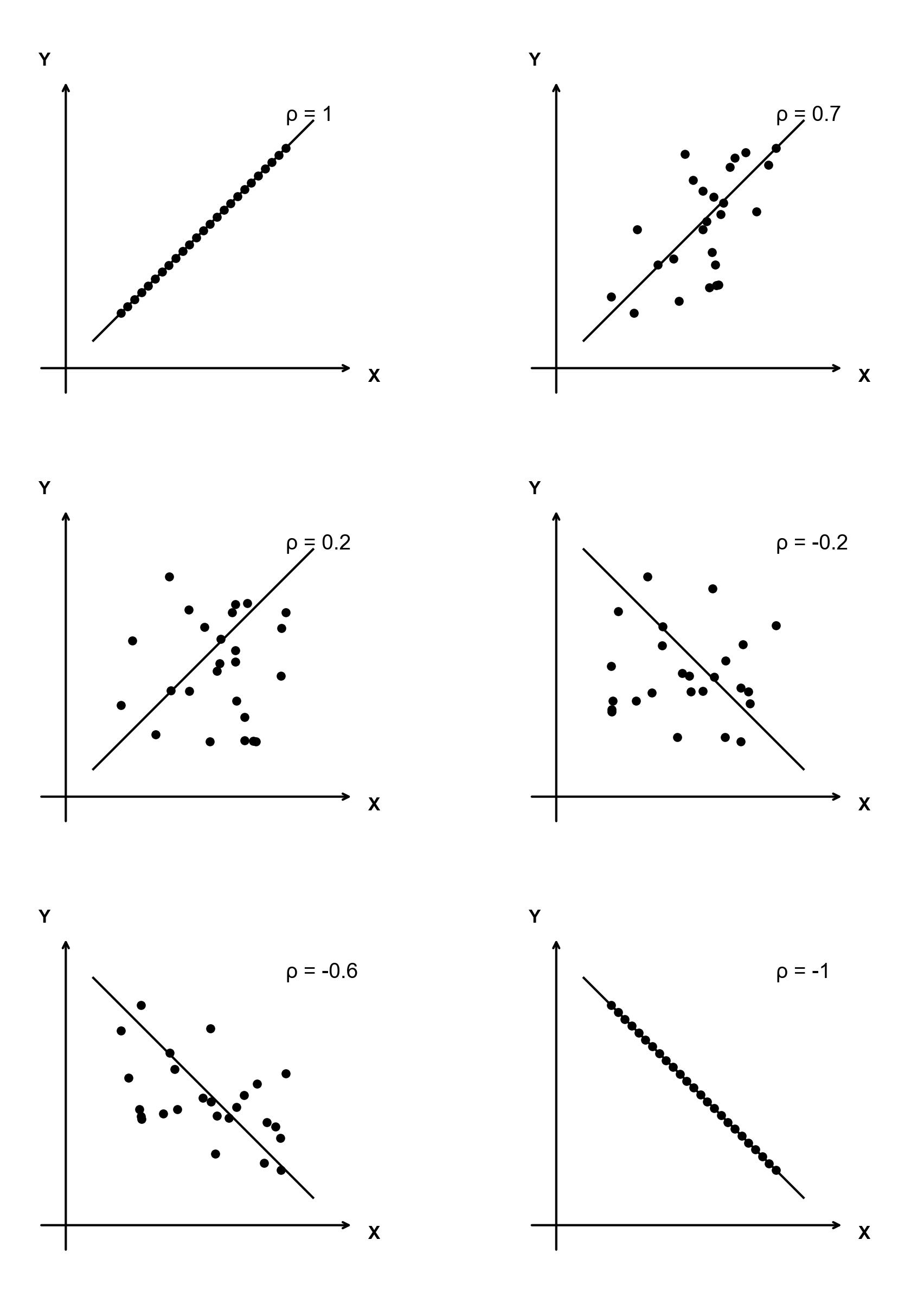
易错：\(Y=-X+3\) 的相关系数是 \(-1\). \(Y = -\frac{1}{2}X+3\) 的相关系数也是-1而不是 \(-\frac{1}{2}\)

其实，可以证明：只要有 \(Y = aX + b\),那么一定有 \[ \rho_{XY} = \begin{cases} 1, & a > 0 \\ -1, & a < 0 \end{cases} \]

4-9. 不相关与独立

常用结论：

  1. 任意随机变量 \(X\) 与 \(Y\) 相互独立是 \(X\) 与 \(Y\) 不相关的充分不必要条件.(独立可以推出不相关，但不相关不能推出独立)
  2. 对随机变量 \(X, Y\), 有下列等价命题: \[ \rho_{XY} = 0 \Leftrightarrow Cov(X, Y) = 0 \Leftrightarrow EXY = EXEY \Leftrightarrow D(X \pm Y) = DX + DY \]

第五章-大数定理和中心极限定理

%%{init: {'flowchart': {'curve': 'stepAfter'}}}%%
graph LR
    %% 定义隐藏节点样式
    classDef hidden fill:none,stroke:none,width:0px,height:0px
    
    A1("大数定律和中心极限定理")

    %% A1: 主分支 (大数定律 vs 中心极限定理)
    N1[ ]:::hidden
    A1 --- N1
    N1 --> B1(大数定律)
    N1 --> B2(中心极限定理)

    %% B1: 大数定律的分支
    N2[ ]:::hidden
    B1 --- N2
    N2 --> C1(依概率收敛)
    N2 --> C2(切比雪夫大数定律)
    N2 --> C3(辛钦大数定律)
    N2 --> C4(伯努利大数定律)

    %% B2: 中心极限定理的分支
    N3[ ]:::hidden
    B2 --- N3
    N3 --> C5(列维-林德伯格定理)
    N3 --> C6(棣莫弗-拉普拉斯定理)

第六章-数理统计

%%{init: {'flowchart': {'curve': 'stepAfter'}}}%%
graph LR
    %% 定义隐藏节点样式
    classDef hidden fill:none,stroke:none,width:0px,height:0px
    
    A1("数理统计的基本概念")

    %% A1: 主分支
    N1[ ]:::hidden
    A1 --- N1
    N1 --> B1(总体与样本)
    N1 --> B2(经验分布函数)
    N1 --> B3(统计量与统计值)
    N1 --> B4(三大抽样分布)

    %% B3: 统计量与统计值的分支
    N2[ ]:::hidden
    B3 --- N2
    N2 --> C1(常用统计量)
    N2 --> C2(统计量数字特征)

    %% C1: 常用统计量的分支
    N3[ ]:::hidden
    C1 --- N3
    N3 --> D1(样本均值)
    N3 --> D2(样本方差)
    N3 --> D3(样本标准差)
    N3 --> D4(样本k阶原点矩)
    N3 --> D5(样本k阶中心矩)

    %% B4: 三大抽样分布的分支
    N4[ ]:::hidden
    B4 --- N4
    N4 --> C3(卡方分布)
    N4 --> C4(t分布)
    N4 --> C5(F分布)
    N4 --> C6(正态总体抽样分布)

6-1. 总体和样本

作者声明：
个人观点，仅供参考

Written By 欧航
Last Update: